湘教版九年级数学上册 3.4 相似三角形的判定与性质（3） 同步练习
试卷更新日期：2018-10-17 类型：同步测试
一、选择题
-
1. 下列条件中，一定能判断两个等腰三角形相似的是（ ）A、都含有一个40°的内角 B、都含有一个50°的内角 C、都含有一个60°的内角 D、都含有一个70°的内角2. 如图，四边形ABCD是矩形，E是边B超延长线上的一点，AE与CD相交于点F，则图中的相似三角形共有（ ）
A、4对 B、3对 C、2对 D、1对3. 如图，在Rt△ABC中，CD是斜边AB上的高，则下列结论正确的是（ ）
A、BD= AD B、BC2=AB•CD C、AD2=BD•AB D、CD2=AD•BD4. 如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：①∠C=∠E；②△ADE∽△FDB；③∠AFE=∠AFC；④FD=FB．其中正确的结论是（ ）
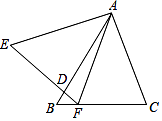A、①③ B、②③ C、①④ D、②④5. 如图，△ABC中，AD是中线，BC=4，∠B=∠DAC，则线段AC的长为（ ）
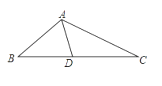A、 B、2 C、3 D、6. 如图，在Rt△ABC中，∠ABC=90°，BD⊥AD于点D，其中 ，则 =（ ）
A、 B、 C、 D、7. 如图，在△ABC中，点D是AB边上的一点，∠ACD=∠B，AD=1，AC=2，若△ADC的面积为0.8，则△BCD的面积为（ ）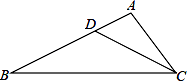
A、0.8 B、1.6 C、2.4 D、3.28. 如图，正方形ABCD边长为8，M，N分别是边BC，CD上的两个动点，且AM⊥MN，则AN的最小值是（ ）
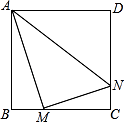A、8 B、4 C、10 D、8二、填空题
-
9. 如图，在△ABC中，∠C=90°，D是AC上一点，DE⊥AB于点E，若AC=8，BC=6，DE=3，则AD的长为 ．
10. 如图，△ABC中，AC=3，BC=4，AB=5，线段DE⊥AB，且△BDE的面积是△ABC面积的三分之一，那么，线段BD长为 ．
11. 如图，在△ABC中，D为AC边上一点，且∠DBA=∠C，若AD=2cm，AB=4cm，那么CD的长等于cm．
12. △ABC中，∠BAC=90°，AD⊥BC于D，图中共有对相似三角形．
13. 如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E．若AB=15，BM=8，则DE的长 ．
14. 如图Rt△ABC中，∠BAC=90°，AB=3，AC=4，点P为BC上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为 ．
15. 如图，在△ABC中，D为AB的中点，E为AC上一点，连接DE，若AB=12，AE=8，∠ABC=∠AED，则AC= ．
16. 如图，在△ABC中，点E，F分别是AC，BC的中点，若S四边形ABFE=9，则S三角形EFC= ．
三、解答题
-
17. 如图所示，已知在Rt△ABC中，CD是斜边AB上的高，若AD=8cm，BD=2cm，求CD的长．
18. 如图，在△ABC中，∠B=∠AED，AB=5，AD=3，CE=6，
求证：
(1)、△ADE∽△ABC；(2)、求AE的长．19. 如图，在矩形ABCD中，DG⊥AC，垂足为G．
(1)、△ADG与△ACD、△CDG与△CAD相似吗？为什么？(2)、若AG=6，CG=12，求矩形ABCD的面积．20. 如图，已知在△ABC中，点D、E分别在边AB、AC上，DE∥BC，点F在DE的延长线上，且∠EAF=∠B，DE=4，EF=5．
(1)、求边AF的长；(2)、如果S△ADE= S△ABC ， 求边BC的长．
