湘教版九年级数学上册 3.4 相似三角形的判定与性质（2）同步练习
试卷更新日期：2018-10-17 类型：同步测试
一、选择题
-
1. 如图，AB∥CD，AE∥FD，则图中的相似三角形共有（ ）
A、2对 B、4对 C、6对 D、8对2. 如图，在△ABC中，已知EF∥BC， = ，四边形BCFE的面积为8，则△ABC的面积等于（ ）
A、9 B、10 C、12 D、133. 如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则 的值为（ ）
A、1 B、 C、 -1 D、 +14. 如图，在菱形ABCD中，点E为边AD的中点，且∠ABC=60°，AB=6，BE交AC于点F，则AF=（ ）
A、1 B、2 C、2.5 D、35. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（ ）
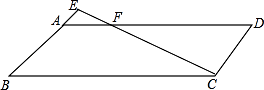
A、3：4 B、9：16 C、9：1 D、3：16. 如图，在▱ABCD中，点E在边AD上，射线CE、BA交于点F，下列等式成立的是（ ）
A、 B、 C、 D、7. 如图，在平行四边形 中，点 在边 上，联结 并延长交 的延长线于点 ，若 ，那么下列结论中正确的是（ ）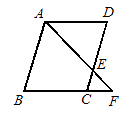
A、 ； B、 ； C、 ； D、 .8. 如图，已知DE∥BC，CD和BE相交于点O，S△DOE：S△COB=9：16，则DE：BC为（ ）
A、2：3 B、3：4 C、9：16 D、1：29. 如图，在▱ABCD中，E为CD上一点，连接AE、BD ， 且AE、BD交于点F ， DE：EC=2：3，则S△DEF：S△ABF=（ ）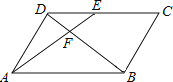
A、2：3 B、4：9 C、2：5 D、4：2510. 在△ABC中，边BC=6，高AD=4，正方形EFGH的顶点E、F在边BC上，顶点H、G分别在边AB和AC上，那么这个正方形的边长等于（ ）
A、3 B、2.5 C、2.4 D、2二、填空题
-
11. 如图，AB∥CD∥EF，则图中相似的三角形有对．
12. 如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F，连接BF．写出图中任意一对相似三角形： ．
13. 如图，△ABC中，D、E分别在AB、AC上，DE∥BC，AD：AB=2：3，则△ADE与△ABC的面积之比为 ．
14. 如图，在▱ABCD中，AC是一条对角线，EF∥BC，且EF与AB相交于点E，与AC相交于点F，3AE=2EB，连接DF．若S△AEF=1，则S△ADF的值为 ．
15. 如图，在△ABC中，DE∥BC， = ，则 = ．
16. 如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF：GF=1：2，那么矩形DEFG的周长是 ．
三、解答题
-
17. 已知如图：DE∥BC，并分别交AB、AC于点D、E．求证：△ADE∽△ABC．
18. 如图，已知△ABC中，四边形DEGF为正方形，D、E在线段AC、BC上，F、G在AB上，如果S△ADF=S△CDE=1，S△BEG=3，求△ABC的面积．
19. 如图，已知梯形上下底边的长分别为36和60，高为32，这个梯形两腰的延长线的交点到两底的距离分别是多少？
20. 如图，在△ABC中，DE∥BC，AD=2cm，BD=3cm．
(1)、求 的值．(2)、若梯形BCED的面积为63cm2 ， 求△ADE的面积．
