2018-2019学年数学七年级上学期期中模拟试卷(深圳专用)
试卷更新日期:2018-10-16 类型:期中考试
一、单选题
-
1. 如果电梯上升5层记为+5.那么电梯下降2层应记为( )A、+2 B、﹣2 C、+5 D、﹣52. 若a、b互为相反数,c为最大的负整数,d的倒数等于它本身,则2a+2b﹣cd的值是( )A、1 B、﹣2 C、﹣1 D、1或﹣13. 下列说法正确的是( )个
a、最大的负整数是-1 ;b、绝对值等于本身的数是正数;c、有理数分为正有理数、负有理数和零;d、数轴上表示-a的点一定在原点左边;e、在数轴上7与9之间的有理数是8.
A、2 B、3 C、4 D、54. 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,…,解答下面问题:2+22+23+24+…+22015﹣1的末位数字是( )A、0 B、3 C、4 D、85. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4 400 000 000人,将这个数用科学记数法表示为( )
A、 B、 C、 D、6. 已知a=5,|b|=8,且满足a+b<0,则a-b的值为( )A、13 B、-13 C、3 D、-37. 下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是( )A、 B、
B、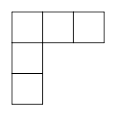 C、
C、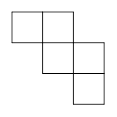 D、
D、 8. 有下列四个算式:
8. 有下列四个算式:①(﹣5)+(+3)=﹣8;
②﹣(﹣2)3=6;
③;
④ .
其中,正确的有( )
A、0个 B、1个 C、2个 D、3个9. 计算2m2n-3m2n的结果为( )
A、-1 B、-23 C、-m2n D、-6m4n210. 用一个平面截下列几何体,截面可能是三角形的是( )①正方体②球体③圆柱④圆锥
A、① B、①② C、①④ D、①③④11. 数轴上的点A到-2的距离是6,则点A表示的数为( )
A、4或-8 B、4 C、-8 D、6或-612. 如果单项式3anb2c是5次单项式,那么n的值为( )
A、2 B、3 C、4 D、5二、填空题
-
13. 若 + 2=0,则xy=14. 李明的练习册上有这样一道题:计算|(-3)+▉|,其中“▉”是被墨水污染而看不到的一个数,他翻看了后边的答案得知该题的计算结果为6,那么“▉”表示的数应该是 .15. 请在〇中填入最大的负整数,△中填入绝对值最小的数,□中填入大于-5且小于3的整数的个数,并将计算结果填在下边的横线上。(〇-△)×□= .
16. 若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 =﹣1,﹣1的差倒数为 ,现已知x1=﹣ ,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则 x2017= .三、计算题
-
17. 计算与化简:(1)、(-9)-(-7)+(-6)-(+4)-(-5)(2)、(3)、18. 先化简,再求值:
(1)、4a+3a2-3-3a3-(-a+4a3),其中a=-2;
(2)、2x2y-2xy2-[(-3x2y2+3x2y)+(3x2y2-3xy2)],其中x=-1,y=2.
19. 一个由几个相同的小立方体搭成的几何体的俯视图如图所示,方格里的数字表示该位置的小立方体的个数,请你画出这个几何体的主视图和左视图. 20. 已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.(1)、问多少秒后,甲到A,B,C的距离和为40个单位?(2)、若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?(3)、在(1)(2)的条件下,当甲到A、B、C的距离和为40个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
20. 已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.(1)、问多少秒后,甲到A,B,C的距离和为40个单位?(2)、若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?(3)、在(1)(2)的条件下,当甲到A、B、C的距离和为40个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.