2018-2019学年人教版九年级数学上学期期中模拟
试卷更新日期:2018-10-16 类型:期中考试
一、单选题
-
1. 将一元二次方程x2+3=x化为一般形式后,二次项系数和一次项系数分别为( )A、0、3 B、0、1 C、1、3 D、1、﹣12. 设点A(﹣1,y1)、B(1,y2)、C(2,y3)是抛物线y=﹣2(x﹣1)2+m上的三点,则y1、y2、y3的大小关系正确的是( )A、y2>y3>y1 B、y1>y2>y3 C、y3>y2>y1 D、y1>y3>y23. 下列交通标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
4. 已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A、﹣3 B、3 C、﹣1 D、15. 某城市2014年底已有绿化面积300公顷,经过两年绿化,绿化面积逐年增加,到2016年底增加到363公顷,设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )A、300(1+x)=363 B、300(1+x)2=363 C、300(1+2x)=363 D、363(1-x)2=3006. 在同一坐标系中,作y=x2 , y=- x2 , y= x2的图象,它们的共同特点是( )A、抛物线的开口方向向上 B、都是关于x轴对称的抛物线,且y随x的增大而增大 C、都是关于y轴对称的抛物线,且y随x的增大而减小 D、都是关于y轴对称的抛物线,有公共的顶点7. 二次函数y=x2﹣(12﹣k)x+12,当x>1时,y随着x的增大而增大,当x<1时,y随着x的增大而减小,则k的值应取( )A、12 B、11 C、10 D、98. 在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )A、(﹣4,3) B、(﹣3,4) C、(3,﹣4) D、(4,﹣3)9. 把二次函数y=﹣x2﹣x+3用配方法化成y=a(x﹣h)2+k的形式时,应为( )A、y=﹣(x﹣2)2+2 B、y=﹣(x﹣2)2+4 C、y=﹣(x+2)2+4 D、y=﹣(x﹣)2+310. 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为( )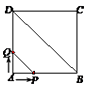 A、
A、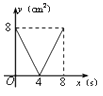 B、
B、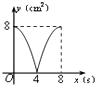 C、
C、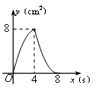 D、
D、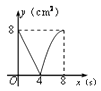
二、填空题
-
11. 下列图形中,①等腰三角形;②平行四边形;③等腰梯形;④圆;⑤正六边形;⑥菱形;⑦正五边形,是中心对称图形的有(填序号)12. 若抛物线y=2x2+mx+8与x轴只有一个公共点,则m的值为 .13. 关于x的一元二次方程x2﹣3x﹣m=0有两个不相等的实数根,则m的取值范围 .14. 若关于x的一元二次方程(a﹣1)x2﹣x+1=0有实数根,则a的取值范围为 .15. 文具店销售某种笔袋,每个18元,小华去购买这种笔袋,结账时店员说:“如果你再多买一个就可以打九折,价钱比现在便宜36元”,小华说:“那就多买一个吧,谢谢,”根据两人的对话可知,小华结账时实际付款元.16. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号).
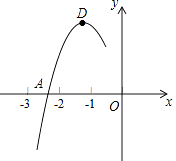
三、解答题
-
17. 解方程:
(1)、(x+6)2=9;(2)、3x2﹣8x+4=0;(3)、(2x﹣1)2=(x﹣3)2 .18. 参加足球联赛的每两队之间都要进行一场比赛,共要比赛28场,共有多少个队参加足球联赛?
19. 巴中市某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售,若两次下调的百分率相同,求平均每次下调的百分率.20. 抛物线y=-x2+bx+c过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.21. 已知关于x的方程x2-2(k-1)x+k2=0有两个实数根x1 , x2 .
⑴求k的取值范围;
⑵若|x1+x2|=x1x2-1,求k的值.22. 已知关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2(1)求m的取值范围并证明x1x2=m+2;
(2)若|x1﹣x2|=2,求m的值.
23. 某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.(Ⅰ)求y与x的函数关系式,并直接写出自变量x的取值范围;求x为何值时y的值为1920?
(Ⅱ)每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
24. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
②若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
25. 温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)、若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;(2)、若建成后的寝室可供600人住宿,求单人间的数量;(3)、若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?26. 如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.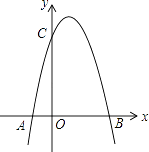 (1)、求点C的坐标;(2)、求这个二次函数的解析式,并求出该函数的最大值.
(1)、求点C的坐标;(2)、求这个二次函数的解析式,并求出该函数的最大值.