2018-2019学年人教版八年级数学上学期期中模拟
试卷更新日期：2018-10-16 类型：期中考试
一、单选题
-
1. 下面4个汽车标志图案，其中不是轴对称图形的是（ ）
A、
B、
C、
D、
2. 下列长度的三条线段首尾连接不能组成三角形的是（ ）A、2，3，5 B、5，5，5 C、6，6，8 D、7，8，93. 某商店出售下列四种形状的地砖：①正三角形； ②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（ ）
A、4种 B、3种 C、2种 D、1种4. 如图，工人师傅安装门时，常用木条EF固定长方形门框ABCD，使其不变形，这种做法的依据是（ ）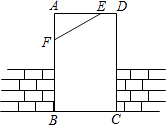
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、三角形的稳定性5. 如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（ ）A、六边形 B、五边形 C、四边形 D、三角形6. 如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
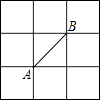A、6 个 B、7 个 C、8 个 D、9个7. 点M（3，﹣2）关于y轴对称的点的坐标为（ ）A、（﹣3，2） B、（﹣3，﹣2） C、（3，﹣2） D、（2，﹣3）8. 如图，已知AC与BD相交于点O，OA=OC，OB=OD，则图中有多少对三角形全等（ ）
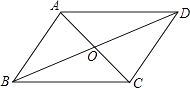A、1 B、2 C、3 D、49. 如图，AB=AC，添加下列条件，不能使△ABE≌△ACD的是（ ）
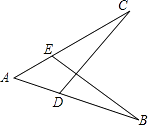A、∠B=∠C B、∠AEB=∠ADC C、AE=AD D、BE=DC10. 如果AD是△ABC的中线，那么下列结论一定成立的有（ ）①BD=CD；②AB=AC；③S△ABD= S△ABC ．
A、3个 B、2个 C、1个 D、0个二、填空题
-
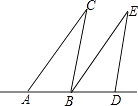
11. 如图，将△ABC沿直线AB向右平移到达△BDE的位置，若∠CAB=55°，∠ABC=100°，则∠CBE的度数为 ．
12. 已知△ABC的两条边的长度分别为3cm，6cm，若△ABC的周长为偶数，则第三条边的长度是 cm．13. 如果点P（4，﹣5）和点Q（a，b）关于y轴对称，则a+b= ．14. 一个n边形的每一个外角都是60°，则这个n边形的内角和是15.如图，DE是三角形ABC的边AB的垂直平分线，分别交AB、BC于D、E，AE平分∠BAC，若∠B=30度，则∠C= 度．
16. 如图，已知△ABC的周长为27cm，AC=9cm，BC边上中线AD=6cm，△ABD周长为19cm，AB= ．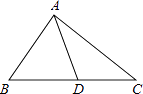
三、解答题
-
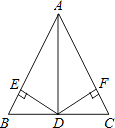
17. 先化简，再求值 ，其中 ．18. 已知等腰三角形的周长是14cm．若其中一边长为4cm，求另外两边长．19. 如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于F，BE=CF.求证：AD是△ABC的角平分线.
20. 如图，已知DA⊥AB，DE平分∠ADC，CE平分 ∠BCD， ∠1+ ∠2=90°．求证：BC ⊥ AB．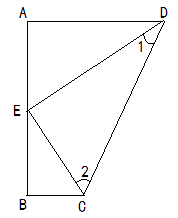
21. 如图，∠AOB=30°，点P是∠AOB内一点，PO=8，在∠AOB的两边分别有点R、Q（均不同于O），求△PQR周长的最小值．
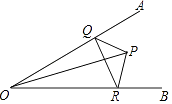22. 如图，点D为码头，A，B两个灯塔与码头的距离相等，DA，DB为海岸线。一轮船离开码头，计划沿∠ADB的角平分线航行，在航行途中C点处，测得轮船与灯塔A和灯塔B的距离相等。试问：轮船航行是否偏离指定航线？请说明理由。
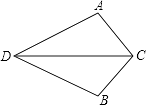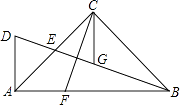
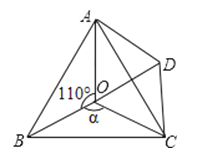
23.如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α，将△BOC绕点C顺时针方向旋转60°，到△ADC，连接OD．
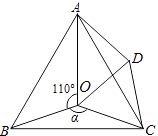(1)、求证：△COD是等边三角形；(2)、当α=150°时，试判断△AOD的形状，并说明理由．(3)、探索：当α为多少度时，△AOD是等腰三角形．24. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．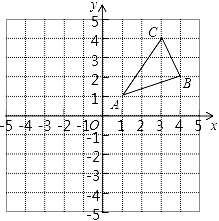
①请画出△ABC关于y轴对称的△A1B1C1；
②请画出△ABC关于x对称的△A2B2C2的各点坐标；
③在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出点P的坐标．
