2018-2019学年人教版七年级数学上学期期中模拟
试卷更新日期：2018-10-16 类型：期中考试
一、单选题
-
1. 给出四个实数 ，2，0，-1，其中负数是（ ）A、 B、2 C、0 D、-12. 如果温度上升10℃记作+10℃，那么温度下降5℃记作（ ）
A、+10℃ B、﹣10℃ C、+5℃ D、﹣5℃3. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4 400 000 000人，将这个数用科学记数法表示为（ ）
A、 B、 C、 D、4. 下列各式中是整式但不是单项式的是（ ）A、 B、 C、 D、5. 若|x﹣1|+|y+2|+|z﹣3|=0．则x+y+z的值为（ ）A、2 B、﹣2 C、0 D、66. 下列计算正确的是（ ）A、3a﹣2a=1 B、x2y﹣2xy2=﹣xy2 C、3a2+5a2=8a4 D、3ax﹣2xa=ax7. 多项式 x|m|−(m−4)x+7是关于x的四次三项式，则m的值是（ ）
A、4 B、-2 C、-4 D、4或-48. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，则图中点C对应的数是（ ）
A、﹣2 B、0 C、1 D、49. 如图所示的运算程序中，若开始输入的x值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，…第2017次输出的结果为（ ）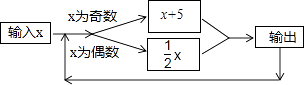
A、3 B、6 C、4 D、2二、填空题
-
10. 在 ， ， ， ， 这五个数中，有理数有个11. 若|x|=2且x＜0，则x= ．12. 若多项式 x|m|－(m＋2)x＋7是关于x的二次三项式，则m＝ ．
13. 若m，n分别表示一个有理数，且m，n互为相反数，则|m+（-2）+n|=.14. 在数轴上，点 所表示的数为2，那么到点 的距离等于3个单位长度的点所表示的数是.
15. 有理数a，b，c在数轴上的对应点如图所示，计算a－b＋c0(填“＞”“＜”或“＝”)．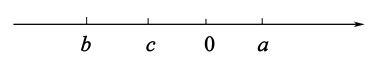
三、解答题
-
16. 已知多项式﹣3x3y|m+1|+xy3+（n﹣2）x2y2﹣4是六次三项式，求（m+1）2n﹣3的值．
17. 有理数a，b，c在数轴上的位置如图所示，化简：|b﹣a|﹣|c﹣b|+|a+b|．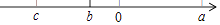
18. 用“⊕”定义一种新运算：对于有理数a和b，规定a⊕b=2a+b，如1⊕3=2×1+3=5(1)、求2⊕（﹣2）的值；(2)、若[（ ）⊕（﹣3）]⊕ =a+4，求a的值．19. 观察下列式子：2×4+1=32；4×6+1=52；6×8+1=72；…．（1）请你以上规律写出第4个等式 ；
（2）根据你发现的规律，请写出第n个等式 ；
（3）你认为（2）中所写的等式一定成立吗？并说明理由．
20.如图，在数轴上点A、B、C表示的数分别为﹣2、1、6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC
（1）请直接写出AB、BC、AC的长度；
（2）若点D从A点出发，以每秒1个单位长度的速度向左运动，点E从B点出发以每秒2个单位长度的速度向右运动，点F从C点出发以每秒5个单位长度的速度向右运动．设点D、E、F同时出发，运动时间为t秒，试探索：EF﹣DE的值是否随着时间t的变化而变化？请说明理由．
（3）若点M以每秒4个单位的速度从A点出发，点N以每秒3个单位的速度运动从C点出发，设点M、N同时出发，运动时间为t秒，试探究：经过多少秒后，点M、N两点间的距离为14个单位．
21.如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
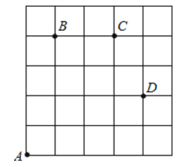(1)、A→C（ ， ），B→D（ ， ）(2)、若这只甲虫按最短路径行走的路线为A→B→C→D，请计算该甲虫走过的路程；(3)、若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+1，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P的位置．