四川省广元市2018年中考数学试卷

试卷更新日期：2018-10-12 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列四个数中，最大的数是（）

A、1 B、 $- 1$ C、0 D、 $\sqrt{2}$

查看试题解析
2. “若 $a$ 是实数，则 $| a |$ ≥0”这一事件是（）

A、必然事件 B、不可能事件 C、不确定事件 D、随机事件

查看试题解析
3.
下面的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有（　　）

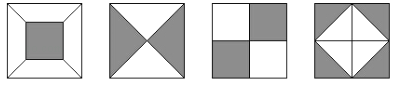A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向平行行驶，那么这两个拐弯的角度可能是（）

A、先向左转130°，再向左转50° B、先向左转50°，再向右转50° C、先向左转50°，再向右转40° D、先向左转50°，再向左转40°

查看试题解析
5. 若二次函数 $y = a x^{2} + b x + a^{2} - 2$ （ $a$ ， $b$ 为常数）的图象如图，则 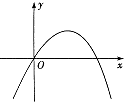$a$ 的值为（）

A、1 B、 $\sqrt{2}$ C、 $- \sqrt{2}$ D、-2

查看试题解析
6. 若以A(－0.5，0)，B(2，0)，C(0，1)三点为顶点画平行四边形，则第四个顶点不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 一组数据2，3，6，8，x的众数是x，其中x是不等式组 ${\begin{matrix} 2 x - 4 > 0 \\ x - 7 < 0 \end{matrix}$ 的整数解，则这组数据的中位数可能是（）

A、3 B、4 C、6 D、3或6

查看试题解析
8. 如图，A，B是⊙O上两点，若四边形ACBO是菱形，⊙O的半径为r，则点A与点B之间的距离为（）

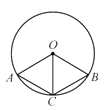A、 $\sqrt{2}$ r B、 $\sqrt{3}$ r C、r D、2r

查看试题解析
9. 如图，点A的坐标为（-1，0），点B在直线 $y = x$ 上运动，当线段AB最短时，点B的坐标为（）

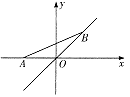A、（0，0） B、（ $- \frac{1}{2}$ ， $- \frac{1}{2}$ ） C、（ $\frac{\sqrt{2}}{2}$ ， $- \frac{\sqrt{2}}{2}$ ） D、（ $- \frac{\sqrt{2}}{2}$ ， $- \frac{\sqrt{2}}{2}$ ）

查看试题解析
10. 已知关于 $x$ 的方程 ${(x + 1)}^{2} + {(x - b)}^{2} = 2$ 有唯一实数解，且反比例函数 $y = \frac{1 + b}{x}$ 的图象在每个象限内 $y$ 随 $x$ 的增大而增大，那么反比例函数的关系式为（）

A、 $y = - \frac{3}{x}$ B、 $y = \frac{1}{x}$ C、 $y = \frac{2}{x}$ D、 $y = - \frac{2}{x}$

查看试题解析

二、填空题

11. 函数 $y = \frac{1}{x - 1}$ 中，自变量x的取值范围是．

查看试题解析
12. 平面上有⊙O及一点P，P到⊙O上一点的距离最长为6cm，最短为2cm，则⊙O的半径为cm．

查看试题解析
13. 分解因式： $3 m^{3} - 18 m^{2} n + 27 m n^{2}$ =

查看试题解析
14. 已知等腰三角形的一个内角为80°，则另两个角的度数是．

查看试题解析
15. 已知一次函数 $y = k x + b$ ，其中 $k$ 从1，-2中随机取一个值， $b$ 从-1，2，3中随机取一个值，则该一次函数的图象经过一，二，三象限的概率为

查看试题解析

三、解答题

16. 计算： $2 cos 45 ° - {(- \frac{1}{4})}^{- 1} - \sqrt{8} - {(π - \sqrt{3})}^{0}$

查看试题解析
17. 已知 $\frac{1}{a - 1}$ ＝2，请先化简 $(1 - \frac{1}{a + 2})$ ÷ $\frac{a^{2} + 2 a + 1}{a^{2} - 4}$ ，再求该式子的值．

查看试题解析
18. 如图，在△AEC和△DFB中，∠E＝∠F，点A，B，C，D在同一直线上，有如下三个关系式：①AE∥DF，②AB＝CD，③CE＝BF.

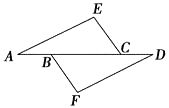(1)、请用其中两个关系式作为条件，另一个作为结论，写出你认为正确的所有命题(用序号写出命题书写形式：“如果⊗，⊗，那么⊗”)；

(2)、选择(1)中你写出的一个命题，说明它正确的理由．

查看试题解析
19. 如图，A，B两座城市相距100千米，现计划要在两座城市之间修筑一条高等级公路（即线段AB）。经测量，森林保护区中心P点在A城市的北偏东30°方向，B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心，50千米为半径的圆形区域内，请问：计划修筑的这条高等级公路会不会穿越保护区？为什么？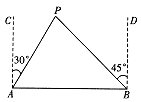

查看试题解析
20. 某乡镇要在生活垃圾存放区建一个老年活动中心，这样必须把1200立方米的生活垃圾运走：

(1)、假如每天能运x立方米，所需时间为y天，写出y与x之间的函数表达式；

(2)、若每辆拖拉机一天能运12立方米，则5辆这样的拖拉机要用多少天才能运完？

(3)、在（2）的情况下，运了8天后，剩下的任务要在不超过6天的时间内完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？

查看试题解析
21. 市教育局行政部门对某县八年级学生的学习情况进行质量监测，在抽样分析中把有一道四选一的单选题的答题结果绘制成了如下两个统计图。请你根据图中信息，解决下列问题：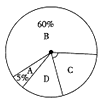

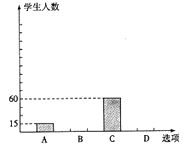(1)、一共随机抽样了多少名学生？

(2)、请你把条形统计图补充完整；

(3)、在扇形统计图中，该县八年级学生选C的所对应圆心角的度数是多少？

(4)、假设正确答案是B，如果该县区有5000名八年级学生，请估计本次质量监测中答对此道题的学生大约有多少名？

查看试题解析
22. 某中心城市有一楼盘，开发商准备以每平方米7000元价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售．

(1)、求平均每次下调的百分率；

(2)、房产销售经理向开发商建议：先公布下调5%，再下调15%，这样更有吸引力，请问房产销售经理的方案对购房者是否更优惠？为什么？

查看试题解析
23. 如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD于点D．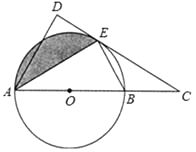

(1)、求证：AE平分∠DAC；

(2)、若AB=4，∠ABE=60°．
①求AD的长；
②求出图中阴影部分的面积.

查看试题解析
24. 如图，在矩形ABCO中，AO=3，tan∠ACB= $\frac{4}{3}$ ，以O为坐标原点，OC为 $x$ 轴，OA为 $y$ 轴建立平面直角坐标系。设D，E分别是线段AC，OC上的动点，它们同时出发，点D以每秒3个单位的速度从点A向点C运动，点E以每秒1个单位的速度从点C向点O运动，设运动时间为 $t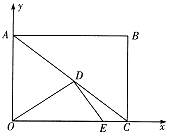$ 秒。

(1)、求直线AC的解析式；

(2)、用含 $t$ 的代数式表示点D的坐标；

(3)、当 $t$ 为何值时，△ODE为直角三角形？

(4)、在什么条件下，以Rt△ODE的三个顶点能确定一条对称轴平行于 $y$ 轴的抛物线？并请选择一种情况，求出所确定抛物线的解析式.

查看试题解析