黑龙江省大庆市林甸县2016-2017学年八年级下学期数学期末模拟试卷
试卷更新日期:2018-10-12 类型:期末考试
一、单选题
-
1. 我国传统文化中的“福禄寿喜”图(如图)由四个图案构成.这四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若代数式 在实数范围内有意义,则实数a的取值范围为( )A、a=4 B、a>4 C、a<4 D、a≠43. 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )
2. 若代数式 在实数范围内有意义,则实数a的取值范围为( )A、a=4 B、a>4 C、a<4 D、a≠43. 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( ) A、 B、 C、 D、4. 下列命题为假命题的个数有( )
A、 B、 C、 D、4. 下列命题为假命题的个数有( )① 相等的角是对顶角;
② 依次连结四边形四边中点所组成的图形是平行四边形;
③ 在同圆或等圆中,相等的弦所对的圆周角相等;
④ 在同圆中,平分弦的直径垂直于这条弦。
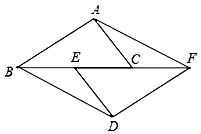
A、0个 B、1个 C、2个 D、3个5. 若分式 中的a、b的值同时扩大到原来的3倍,则分式的值( )A、不变 B、是原来的3倍 C、是原来的6倍 D、是原来的9倍6. 如图,在▱ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC=5,则AE:EF:FB为( )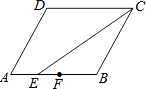 A、1:2:3 B、2:1:3 C、3:2:1 D、3:1:27. 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A、1:2:3 B、2:1:3 C、3:2:1 D、3:1:27. 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )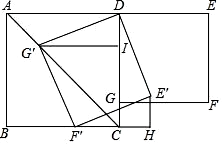 A、 B、 C、 D、8. 已知x2﹣x﹣1=0,则x3﹣2x+1的值是( )
A、 B、 C、 D、8. 已知x2﹣x﹣1=0,则x3﹣2x+1的值是( )
A、1 B、2 C、3 D、49. 一次函数y=ax+3与y=bx﹣1的图象如图所示,其交点B(﹣3,m),则不等式ax﹣bx+3>﹣1的解集表示在数轴上正确的是( ) A、
A、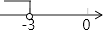 B、
B、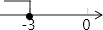 C、
C、 D、
D、 10. 若关于x的分式方程 的解为非负数,则a的取值范围是( )
10. 若关于x的分式方程 的解为非负数,则a的取值范围是( )
A、a≥1 B、a>1 C、a≥1且a≠4 D、a>1且a≠4二、填空题
-
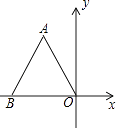
11. 分解因式:m2+2m= .12. 不等式9﹣3x>0的非负整数解是 .13. 正八边形的每个外角的度数为 .14. 四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需满足的条件是(横线只需填一个你认为合适的条件即可)15. 不等式 的解集是 .16. 在等腰△ABC中,AD⊥BC交直线BC于点D,若AD= BC,则△ABC的顶角的度数为 .17. 如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为 .
三、解答题
-
18. 解不等式组 .
19. 先化简,再求值: ,其中x= +1.
20.(1)、计算: +|3﹣ |﹣2sin60°+(2017﹣π)0+( )﹣2(2)、解方程: .21. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题: (1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出A1的坐标.
(1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出A1的坐标.
(2)、画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2 , 并写出A2的坐标.
(3)、画出△A2B2C2关于原点O成中心对称的△A3B3C3 , 并写出A3的坐标.
22. 如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.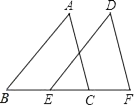 23. 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
23. 如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.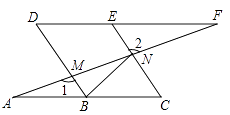 (1)、求证:四边形BCED是平行四边形;(2)、已知DE=2,连接BN,若BN平分∠DBC,求CN的长.24. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)、求证:四边形BCED是平行四边形;(2)、已知DE=2,连接BN,若BN平分∠DBC,求CN的长.24. 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.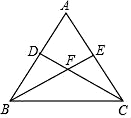 (1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.25. 如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
(1)、判断∠ABE与∠ACD的数量关系,并说明理由;(2)、求证:过点A、F的直线垂直平分线段BC.25. 如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.