山东省济南市2018年中考数学试卷
试卷更新日期:2018-10-12 类型:中考真卷
一、选择题
-
1. 4的算术平方根为( )
A、2 B、-2 C、±2 D、162. 如图,点O在直线AB上,若∠1=40°,则∠2的度数是( ) A、50° B、60° C、140° D、150°3. 下列运算中,结果是 的是( )
A、50° B、60° C、140° D、150°3. 下列运算中,结果是 的是( )
A、 B、a10÷a2 C、(a2)3 D、(-a)54. 我国成功发射了嫦娥三号卫星,是世界上第三个实现月面软着陆和月面巡视探测的国家,嫦娥三号探测器的发射总质量约为3700千克,3700用科学记数法表示为( )A、3.7×102 B、3.7×103 C、37×102 D、0.37×1045. 下列图案既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
6. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( ) A、从前面看到的形状图的面积为5 B、从左面看到的形状图的面积为3 C、从上面看到的形状图的面积为3 D、三种视图的面积都是47. 化简 的结果是( )
A、从前面看到的形状图的面积为5 B、从左面看到的形状图的面积为3 C、从上面看到的形状图的面积为3 D、三种视图的面积都是47. 化简 的结果是( )
A、 B、 C、 D、8. 下列命题中,真命题是 ( )
A、两对角线相等的四边形是矩形 B、两对角线互相平分的四边形是平行四边形 C、两对角线互相垂直的四边形是菱形 D、两对角线相等的四边形是等腰梯形9. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、10. 在▱ABCD中,延长AB到E,使BE=AB,连结DE交BC于F,则下列结论不一定成立的是( ) A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF11. 学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是( )A、 B、 C、 D、12. 如图,直线 与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( )
A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF11. 学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是( )A、 B、 C、 D、12. 如图,直线 与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( ) A、( ,3) B、( , ) C、(2, ) D、( ,4)13. 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
A、( ,3) B、( , ) C、(2, ) D、( ,4)13. 如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是( )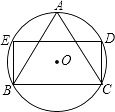 A、2 B、 C、 D、14. 现定义一种变换:对于一个由有限个数组成的序列S0 , 将其中的每个数换成该数在S0中出现的次数,可得到一个新序列S1 , 例如序列S0:(4,2,3,4,2),通过变换可生成新序列S1:(2,2,1,2,2),若S0可以为任意序列,则下面的序列可作为S1的是( )A、(1,2,1,2,2) B、(2,2,2,3,3) C、(1,1,2,2,3) D、(1,2,1,1,2)15. 二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( )
A、2 B、 C、 D、14. 现定义一种变换:对于一个由有限个数组成的序列S0 , 将其中的每个数换成该数在S0中出现的次数,可得到一个新序列S1 , 例如序列S0:(4,2,3,4,2),通过变换可生成新序列S1:(2,2,1,2,2),若S0可以为任意序列,则下面的序列可作为S1的是( )A、(1,2,1,2,2) B、(2,2,2,3,3) C、(1,1,2,2,3) D、(1,2,1,1,2)15. 二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( )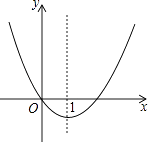 A、t≥﹣1 B、﹣1≤t<3 C、﹣1≤t<8 D、3<t<8
A、t≥﹣1 B、﹣1≤t<3 C、﹣1≤t<8 D、3<t<8二、填空题
-
16. |﹣7﹣3|= .17. 分解因式:x2+2x+1= .
18. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为 ,那么口袋中球的总个数为 .
19. 若 和 的值相等,则 .
20. 如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 21. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,若 ,则 的值为.
21. 如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,若 ,则 的值为.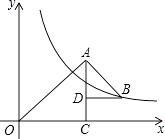
三、解答题
-
22.
(1)、化简:(a+3)(a-3)+a(4-a)
(2)、解不等式组: .23.
(1)、如图,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC. (2)、如图,AB与 相切于C, ,⊙O的半径为6,AB=16,求OA的长.
(2)、如图,AB与 相切于C, ,⊙O的半径为6,AB=16,求OA的长.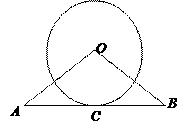 24. 2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
24. 2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
25. 在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:劳动时间(时)
频数(人数)
频率
0.5
12
0.12
1
30
0.3
1.5
x
0.4
2
18
y
合计
m
1
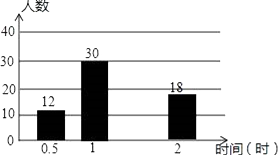
(1)、统计表中的x= , y=;
(2)、被调查同学劳动时间的中位数是时;(3)、请将频数分布直方图补充完整;
(4)、求所有被调查同学的平均劳动时间.
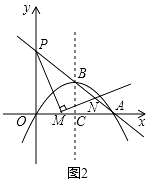
26. 如图1,反比例函数 的图象经过点A( ,1),射线AB与反比例函数图象交与另一点B(1, ),射线AC与 轴交于点C, 轴,垂足为D. (1)、求 和a的值;(2)、直线AC的解析式;(3)、如图2,M是线段AC上方反比例函数图象上一动点,过M作直线 轴,与AC相交于N,连接CM,求 面积的最大值.
(1)、求 和a的值;(2)、直线AC的解析式;(3)、如图2,M是线段AC上方反比例函数图象上一动点,过M作直线 轴,与AC相交于N,连接CM,求 面积的最大值.
27. 如图1,有一组平行线 ,正方形 的四个顶点分别在 上, 过点D且垂直于 于点E,分别交 于点F,G, .
于点E,分别交 于点F,G, . (1)、AE= , 正方形ABCD的边长=;
(1)、AE= , 正方形ABCD的边长=;
(2)、如图2,将 绕点A顺时针旋转得到 ,旋转角为 ,点 在直线 上,以 为边在的 左侧作菱形 ,使点 分别在直线 上.①写出 与 的函数关系并给出证明;
②若 =30°,求菱形 的边长.
28. 如图1,抛物线 平移后过点A(8,0)和原点,顶点为B,对称轴与 轴相交于点C,与原抛物线相交于点D.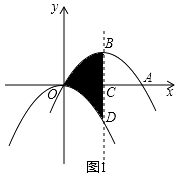
 (1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:
(1)、求平移后抛物线的解析式并直接写出阴影部分的面积 ;(2)、如图2,直线AB与 轴相交于点P,点M为线段OA上一动点, 为直角,边MN与AP相交于点N,设 ,试探求:① 为何值时 为等腰三角形;
②
 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.