辽宁省锦州市2018年中考数学试卷
试卷更新日期:2018-10-12 类型:中考真卷
一、选择题
-
1. 下列实数为无理数的是( )
A、-5 B、 C、0 D、π2. 如图,这是由5个大小相同的整体搭成的几何体,该几何体的左视图是 ( ) A、
A、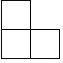 B、
B、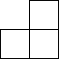 C、
C、 D、
D、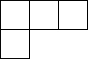 3. 一元二次方程2x2-x+1=0的根的情况是( )
3. 一元二次方程2x2-x+1=0的根的情况是( )
A、两个不相等的实数根 B、两个相等的实数根 C、没有实数根 D、无法判断4. 为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳比赛,下列统计量中能用来比较两人成绩稳定程度的是( )
A、平均数 B、中位数 C、众数 D、方差5. 如图,直线l1∥l2 , 且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°,则∠2的度数为( )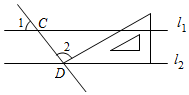 A、92° B、98° C、102° D、108°6. 下列计算正确的是( )A、7a-a=6 B、a2·a3=a5 C、(a3)3=a6 D、(ab)4=ab47. 如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF= ,则AE2+BE2的值为( )
A、92° B、98° C、102° D、108°6. 下列计算正确的是( )A、7a-a=6 B、a2·a3=a5 C、(a3)3=a6 D、(ab)4=ab47. 如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF= ,则AE2+BE2的值为( )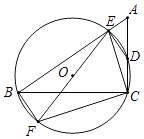 A、8 B、12 C、16 D、208. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A、8 B、12 C、16 D、208. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )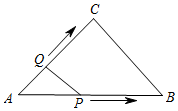 A、
A、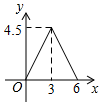 B、
B、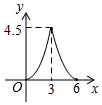 C、
C、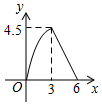 D、
D、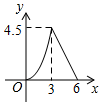
二、填空题
-
9. 因式分解:x3﹣4x= .
10. 上海合作组织青岛峰会期间,为推进“一带一路”建设,中国决定在上海合作组织银行联合体框架内,设立300亿元人民币等值专项贷款.将300亿元用科学记数法表示为元.
11. 如图,这是一幅长为3m,宽为2m的长方形世界杯宣传画.为测量画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4附近,由此可估计宣传画上世界杯图案的面积为m2. 12. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为.
12. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为. 13. 如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+a<bx-4的解集是.
13. 如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+a<bx-4的解集是.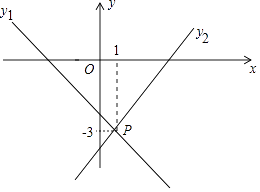 14. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为.
14. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为.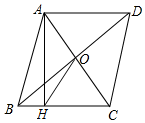 15. 如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数 (k≠0)的图象经过P,B两点,则k的值为.
15. 如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数 (k≠0)的图象经过P,B两点,则k的值为.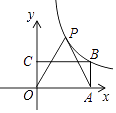 16. 如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A,作线段 OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB.以AB为边在△AOB的外侧作正方形ABCA1 , 延长A1C交射线OB于点B1 , 以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2 , 延长A2C1交射线OB于点B2 , 以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去,则正方形A2017B2017C2017A2018的周长为.
16. 如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A,作线段 OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB.以AB为边在△AOB的外侧作正方形ABCA1 , 延长A1C交射线OB于点B1 , 以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2 , 延长A2C1交射线OB于点B2 , 以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去,则正方形A2017B2017C2017A2018的周长为.
三、解答题
-
17. 先化简,再求值: , 其中x=318. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表.
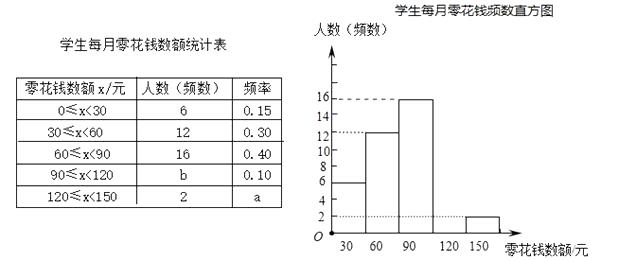
请根据以上图表,解答下列问题:
(1)、这次被调查的人数共有人,a=;
(2)、计算并补全频数分布直方图;
(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.
19. 动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)、姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为;
(2)、若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率. 20. 为迎接“七·一”党的生日,某校准备组织师生共310人参加一次大型公益活动,租用4辆大客车和6辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多15个.
20. 为迎接“七·一”党的生日,某校准备组织师生共310人参加一次大型公益活动,租用4辆大客车和6辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多15个.
(1)、求每辆大客车和小客车的座位数;(2)、经学校统计,实际参加活动人数增加了40人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为使所有参加活动的师生均有座位,最多租用小客车多少辆?
21. 如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4, ≈1.4) 22. 如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
22. 如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF. (1)、求证:BC是⊙O的切线;(2)、若sin∠EFA= ,AF= ,求线段AC的长.23. 某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:
(1)、求证:BC是⊙O的切线;(2)、若sin∠EFA= ,AF= ,求线段AC的长.23. 某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:每个商品的售价x(元)
…
30
40
50
…
每天的销售量y个
…
100
80
60
…
(1)、求y与x之间的函数关系式;(2)、设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)、不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?24. 如图1,以▱ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G. (1)、猜想BG与EG的数量关系.并说明理由;
(1)、猜想BG与EG的数量关系.并说明理由;
(2)、延长DE,BA交于点H,其他条件不变,①如图2,若∠ADC=60°,求 的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出 的值.(用含α的三角函数表示)
25. 在平面直角坐标系中,直线 与x轴交于点B,与y轴交于点C,二次函数 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.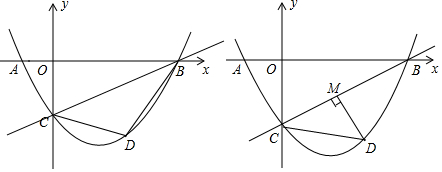 (1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.