黑龙江省大庆六十一中2016-2017学年八年级下学期数学期末考试试卷(五四学制)
试卷更新日期:2018-10-12 类型:期末考试
一、单选题
-
1. 已知= , 那么的值为( )A、 B、 C、 D、2. 如图所示的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
3. 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )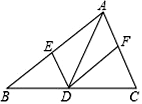 A、若AD⊥BC,则四边形AEDF是矩形 B、若AD垂直平分BC,则四边形AEDF是矩形 C、若BD=CD,则四边形AEDF是菱形 D、若AD平分∠BAC,则四边形AEDF是菱形4. 用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )A、(x+2)2=1 B、(x+2)2=19 C、(x+2)2=13 D、(x+2)2=75. 若双曲线 过两点(﹣1, ),(﹣3, ),则 与 的大小关系为( )
A、若AD⊥BC,则四边形AEDF是矩形 B、若AD垂直平分BC,则四边形AEDF是矩形 C、若BD=CD,则四边形AEDF是菱形 D、若AD平分∠BAC,则四边形AEDF是菱形4. 用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )A、(x+2)2=1 B、(x+2)2=19 C、(x+2)2=13 D、(x+2)2=75. 若双曲线 过两点(﹣1, ),(﹣3, ),则 与 的大小关系为( )
A、 > B、 < C、 = D、y1与y2大小无法确定6. 函数y=(m2﹣m) 是反比例函数,则( )
A、m≠0 B、m≠0且m≠1 C、m=2 D、m=1或27. 已知a、b、c为常数,点P(a,c)在第二象限,则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断8. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、 B、
B、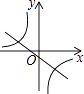 C、
C、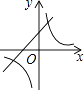 D、
D、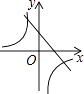 9. 如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2 , 则所修道路的宽度为( )m.
9. 如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2 , 则所修道路的宽度为( )m. A、4 B、3 C、2 D、110. 如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的个数是( )
A、4 B、3 C、2 D、110. 如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的个数是( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 一个四边形的各边之比为1:2:3:4,和它相似的另一个四边形的最小边长为5cm,则它的最大边长为 cm.12. 若方程x2﹣4x+1=0的两根是x1 , x2 , 则x1(1+x2)+x2的值为 .13. 已知三个数1, ,2,请再添上一个数,使它们构成一个比例式,满足这样条件的数是 .14. 一个布袋内只装有一个红球和2个黄球,这些球除颜色外其余都相同,随机摸出一个球后放回搅匀,再随机摸出一个球,则两次摸出的球都是黄球的概率是 .15. 如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为 .
 16. 如图,直线y=﹣x+b与双曲线y=﹣ (x<0)交于点A,与x轴交于点B,则OA2﹣OB2= .
16. 如图,直线y=﹣x+b与双曲线y=﹣ (x<0)交于点A,与x轴交于点B,则OA2﹣OB2= . 17. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .
17. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .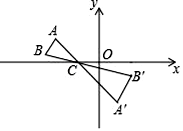 18. 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为 .
18. 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为 .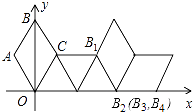
三、解答题
-
19. 解方程:(1)、4x2﹣8x+1=0(2)、(x﹣3)2+2x(x﹣3)=0.20. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?21. 关于x的方程 有两个不相等的实数根.(1)、求实数k的取值范围;(2)、设方程的两个实数根分别为 、 ,存不存在这样的实数k,使得 ?若存在,求出这样的k值;若不存在,说明理由.22. 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
1
根据图表提供的信息,解答下列问题:
 (1)、八年级一班有多少名学生?(2)、请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;(3)、在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.23. 如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
(1)、八年级一班有多少名学生?(2)、请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;(3)、在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.23. 如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.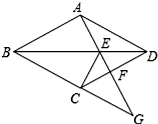 (1)、求证:∠DAE=∠DCE;(2)、当CE=2EF时,EG与EF的等量关系是 .24. 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
(1)、求证:∠DAE=∠DCE;(2)、当CE=2EF时,EG与EF的等量关系是 .24. 如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.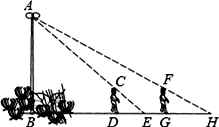 25. 已知:y=y1+y2 , y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时,y=1.求x=﹣ 时,y的值.26. 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D.F分别在边AB、AC上.
25. 已知:y=y1+y2 , y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时,y=1.求x=﹣ 时,y的值.26. 如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D.F分别在边AB、AC上.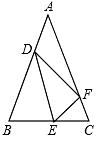 (1)、求证:△BDE∽△CEF;(2)、当点E移动到BC的中点时,求证:FE平分∠DFC.27. 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题:
(1)、求证:△BDE∽△CEF;(2)、当点E移动到BC的中点时,求证:FE平分∠DFC.27. 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题: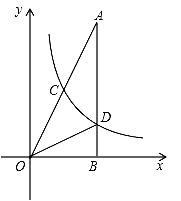 (1)、求反比例函数解析式;(2)、求C点坐标.28. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)、求反比例函数解析式;(2)、求C点坐标.28. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.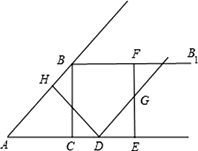 (1)、当t为何值时,AD=AB,并求出此时DE的长度;(2)、当△DEG与△ACB相似时,求t的值.
(1)、当t为何值时,AD=AB,并求出此时DE的长度;(2)、当△DEG与△ACB相似时,求t的值.