湖北省鄂州市2018年中考数学试卷
试卷更新日期:2018-10-12 类型:中考真卷
一、选择题
-
1. 2018的相反数是( )
A、 B、 C、3102 D、-20182. 下列计算正确的是( )
A、 B、 C、 D、若 ,则x=13. 如图,由几个相同的小正方体搭成的一个几何体,它的左视图为( )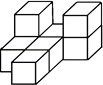 A、
A、 B、
B、 C、
C、 D、
D、 4. 一副三角板有两个直角三角形,如图叠放在一起,则 的度数是( )
4. 一副三角板有两个直角三角形,如图叠放在一起,则 的度数是( ) A、165° B、120° C、150° D、135°5. 下列命题正确的个数是( )
A、165° B、120° C、150° D、135°5. 下列命题正确的个数是( )①若代数式 有意义,则x的取值范围为x≤1且x≠0.②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.③若反比例函数 (m为常数),当x>0时,y随x增大而增大,则一次函数y=-2 x + m的图象一定不经过第一象限.④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y = x2中偶函数的个数为2个.
A、1 B、2 C、3 D、46. 一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则用来表示y与x之间关系的选项是( )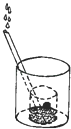 A、
A、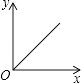 B、
B、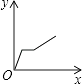 C、
C、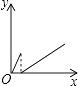 D、
D、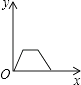 7. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则 = ( )
7. 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则 = ( ) A、 B、 C、 D、8. 已知m,n是关于x的一元二次方程x2-3x+a=0的两个解,若(m-1)(n-1)=-6,则a的值为( )
A、 B、 C、 D、8. 已知m,n是关于x的一元二次方程x2-3x+a=0的两个解,若(m-1)(n-1)=-6,则a的值为( )
A、-10 B、4 C、-4 D、109. 小明从如图所示的二次函数y = ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab > 0 ②a+b+c < 0 ③b+2c > 0 ④a-2b+4c > 0 ⑤ .你认为其中正确信息的个数有( )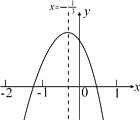 A、2个 B、3个 C、4个 D、5个10. 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A、2个 B、3个 C、4个 D、5个10. 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( ) A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
11. 若|p+3|=0,则p= .
12. 下列几个命题中正确的个数为个.①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4, 5,6).②5名同学的语文成绩为90,92,92,98,103,则他们平均分为95,众数为92.③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定.④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员
个人年创利润/万元
10
8
5
3
员工人数
1
3

4
工个人年创利润的中位数为5万元”的说法无法判断对错.
13. 若不等式组 的解集为3≤x≤4,则不等式ax+b<0的解集为.
14. 已知正比例函数y=-4x与反比例函数y= 的图像交于A,B两点,若点A的坐标为(x,4),则点B的坐标为 .
15. 著名画家达·芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A、B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来.若AB=20cm,则画出的圆的半径为cm.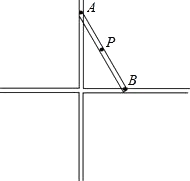 16. 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△ 处,此时线段 与BO的交点E为BO的中点,则线段 的长度为.
16. 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△ 处,此时线段 与BO的交点E为BO的中点,则线段 的长度为.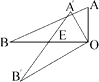
三、解答题
-
17. 先化简,后求值: ,其中a=3.
18. 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.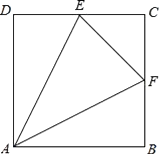 (1)、求证:△ADE≌△ABF.(2)、求△AEF的面积.19. 一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“扬”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)、求证:△ADE≌△ABF.(2)、求△AEF的面积.19. 一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“扬”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)、若从中任取一个球,球上的汉字刚好是“扬”的概率为多少?
(2)、甲从中任取一球,不放回,再从中任取一球,请用画树状图的方法求出甲取出的两个球上的汉字恰能组成“灵秀”或“扬州”的概率P1;
(3)、乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“扬州”的概率为P2 , 指出P1 , P2的大小关系(请直接写出结论,不必证明).
20. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题: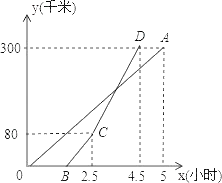 (1)、轿车到达乙地后,货车距乙地多少千米?(2)、求线段CD对应的函数解析式.(3)、轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).21. 小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:
(1)、轿车到达乙地后,货车距乙地多少千米?(2)、求线段CD对应的函数解析式.(3)、轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).21. 小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问: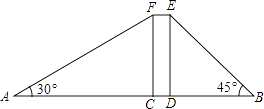 (1)、楼高多少米?(2)、若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: ≈1.73, ≈1.41, ≈2.24)
(1)、楼高多少米?(2)、若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: ≈1.73, ≈1.41, ≈2.24)
22. 已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F. (1)、求证:DE为⊙O的切线.
(1)、求证:DE为⊙O的切线.
(2)、求证:AB:AC=BF:DF.23. 某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)、不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x
销售量y(件)
销售玩具获得利润w(元)
(2)、在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.(3)、在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
24. 在平面直角坐标系中,已知M1(3,2),N1(5,-1),线段M1N1平移至线段MN处(注:M1与M,N1与N分别为对应点). (1)、若M(-2,5),请直接写出N点坐标.(2)、在(1)问的条件下,点N在抛物线 上,求该抛物线对应的函数解析式.(3)、在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC︰OF=2︰ ,求m的值.
(1)、若M(-2,5),请直接写出N点坐标.(2)、在(1)问的条件下,点N在抛物线 上,求该抛物线对应的函数解析式.(3)、在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC︰OF=2︰ ,求m的值.
(4)、在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的 ,求此时BP的长度.