黑龙江伊春市2018年中考数学试卷（农垦、森工用）
试卷更新日期：2018-10-12 类型：中考真卷
一、填空题
-
1. 2018年1月18日，国家统计局对外公布，我国经济总量首次站上80万亿的历史新台阶，将80万亿用科学记数法表示亿元．2. 函数y= 中，自变量x的取值范围是 ．3. 如图，在平行四边形ABCD中，添加一个条件使平行四边形ABCD是菱形．
4. 在一个不透明的袋子中装有除颜色外完全相同的5个红球、3个白球、2个绿球，任意摸出一球，摸到白球的概率是 ．
5. 不等式组 有3个整数解，则a的取值范围是 ．6. 如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO=15°，则∠ACB= ．
7. 用一块半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则此圆锥的高为 ．8. 如图，已知正方形ABCD的边长是4，点E是AB边上一动点，连接CE，过点B作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值为 ．
9. Rt△ABC中，∠ABC=90°，AB=3，BC=4，过点B的直线把△ABC分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是 ．10. 如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1 ， △B2C1B3的面积为S2 ， △B3C2B4的面积为S3 ， 如此下去，则Sn= ．
二、选择题
-
11. 下列各运算中，计算正确的是（ ）A、a12÷a3=a4 B、（3a2）3=9a6 C、（a﹣b）2=a2﹣ab+b2 D、2a•3a=6a212. 如图图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
13. 如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图，则组成这个几何体的小正方体的个数不可能是（ ）
A、3 B、4 C、5 D、614. 某学习小组的五名同学在一次数学竞赛中的成绩分别是94分、98分、90分、94分、74分，则下列结论正确的是（ ）A、平均分是91 B、中位数是90 C、众数是94 D、极差是2015. 某中学组织初三学生篮球比赛，以班为单位，每两班之间都比赛一场，计划安排15场比赛，则共有多少个班级参赛？（ ）
A、4 B、5 C、6 D、716. 已知关于x的分式方程 =1的解是负数，则m的取值范围是（ ）A、m≤3 B、m≤3且m≠2 C、m＜3 D、m＜3且m≠217. 如图，在△ABC中，AB=5，AC=3，BC=4，将△ABC绕A逆时针方向旋转40°得到△ADE，点B经过的路径为弧BD，是图中阴影部分的面积为（ ）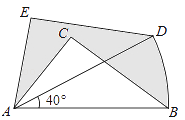
A、 π﹣6 B、 π C、 π﹣3 D、 +π18. 如图，∠AOB=90°，且OA，OB分别与反比例函数y= （x＞0）、y=﹣ （x＜0）的图象交于A，B两点，则tan∠OAB的值是（ ）
A、 B、 C、1 D、19. 为奖励消防演练活动中表现优异的同学，某校决定用1200元购买篮球和排球，其中篮球每个120元，排球每个90元，在购买资金恰好用尽的情况下，购买方案有（ ）A、4种 B、3种 C、2种 D、1种20. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB= BC=1，则下列结论：①∠CAD=30°②BD= ③S平行四边形ABCD=AB•AC④OE= AD⑤S△APO= ，正确的个数是（ ）
A、2 B、3 C、4 D、5三、解答题
-
21. 先化简，再求值：（a﹣ ）÷ ，其中a= ，b=1．22. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．
(1)、①画出△ABC关于x轴对称的△A1B1C1；②画出△ABC绕点O逆时针旋转90°后的△A2B2C2；
(2)、在（1）的条件下，求线段BC扫过的面积（结果保留π）．23. 如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．
(1)、求此抛物线的解析式．
(2)、点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．24. 为响应党的“文化自信”号召，某校开展了古诗词诵读大赛活动，现随机抽取部分同学的成绩进行统计，并绘制成如下的两个不完整的统计图，请结合图中提供的信息，解答下列各题：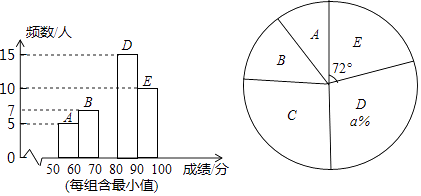
(1)、直接写出a的值，a= ， 并把频数分布直方图补充完整 ．(2)、求扇形B的圆心角度数．(3)、如果全校有2000名学生参加这次活动，90分以上（含90分）为优秀，那么估计获得优秀奖的学生有多少人？
25. 某工厂甲、乙两车间接到加工一批零件的任务，从开始加工到完成这项任务共用了9天，乙车间在加工2天后停止加工，引入新设备后继续加工，直到与甲车间同时完成这项任务为止，设甲、乙车间各自加工零件总数为y（件），与甲车间加工时间x（天），y与x之间的关系如图（1）所示．由工厂统计数据可知，甲车间与乙车间加工零件总数之差z（件）与甲车间加工时间x（天）的关系如图（2）所示．
(1)、甲车间每天加工零件为件，图中d值为 ．
(2)、求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式．
(3)、甲车间加工多长时间时，两车间加工零件总数为1000件？
26. 如图，在Rt△BCD中，∠CBD=90°，BC=BD，点A在CB的延长线上，且BA=BC，点E在直线BD上移动，过点E作射线EF⊥EA，交CD所在直线于点F．
(1)、当点E在线段BD上移动时，如图（1）所示，求证：AE=EF；(2)、当点E在直线BD上移动时，如图（2）、图（3）所示，线段AE与EF又有怎样的数量关系？请直接写出你的猜想，不需证明．27. 为了落实党的“精准扶贫”政策，A、B两城决定向C、D两乡运送肥料以支持农村生产，已知A、B两城共有肥料500吨，其中A城肥料比B城少100吨，从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨；从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨．现C乡需要肥料240吨，D乡需要肥料260吨．
(1)、A城和B城各有多少吨肥料？
(2)、设从A城运往C乡肥料x吨，总运费为y元，求出最少总运费．
(3)、由于更换车型，使A城运往C乡的运费每吨减少a（0＜a＜6）元，这时怎样调运才能使总运费最少？28. 如图，在平面直角坐标系中，菱形ABCD的边AB在x轴上，点B坐标（﹣3，0），点C在y轴正半轴上，且sin∠CBO= ，点P从原点O出发，以每秒一个单位长度的速度沿x轴正方向移动，移动时间为t（0≤t≤5）秒，过点P作平行于y轴的直线l，直线l扫过四边形OCDA的面积为S．
(1)、求点D坐标．(2)、求S关于t的函数关系式．(3)、在直线l移动过程中，l上是否存在一点Q，使以B、C、Q为顶点的三角形是等腰直角三角形？若存在，直接写出Q点的坐标；若不存在，请说明理由．