甘肃省天水市2018年中考数学试卷
试卷更新日期：2018-10-12 类型：中考真卷
一、选择题
-
1. 下列四个数中，小于0的数是（ ）A、﹣1 B、0 C、1 D、π2. 下列计算正确的是（ ）A、a3+a2=2a5 B、（﹣2a3）2=4a6 C、（a+b）2=a2+b2 D、a6÷a2=a33. 下列图形中，中心对称图形有（ ）
A、1个 B、2个 C、3个 D、4个4. 函数y1=x和y2= 的图象如图所示，则y1＞y2的x取值范围是（ ）
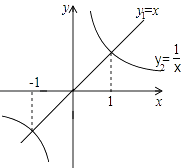A、x＜﹣1或x＞1 B、x＜﹣1或0＜x＜1 C、﹣1＜x＜0或x＞1 D、﹣1＜x＜0或0＜x＜15. 如图，直线l1∥l2 ， 则∠α为（ ）
A、150° B、140° C、130° D、120°6. 一个三角形的两边长分别为3和6，第三边的边长是方程（x﹣2）（x﹣4）=0的根，则这个三角形的周长是（ ）
A、11 B、11或13 C、13 D、以上选项都不正确7. 一组数据：3，2，1，2，2的众数，中位数，方差分别是（ ）A、2，1，0.4 B、2，2，0.4 C、3，1，2 D、2，1，0.28. 从一块正方形的木板上锯掉2 m宽的长方形木条，剩下的面积是48㎡，则原来这块木板的面积是（ ）
A、100㎡ B、64㎡ C、121㎡ D、144㎡9. 如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（ ）
A、OM的长 B、2OM的长 C、CD的长 D、2CD的长10.如图，已知等边三角形ABC的边长为2，E、F、G分别是边AB、BC、CA的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y与x的函数图象大致是（ ）
A、
B、
C、
D、
二、填空题
-
11. 已知点M（3，﹣2），将它先向左平移4个单位，再向上平移3个单位后得到点N，则点N的坐标是 ．12. 从1至9这9个自然数中任取一个数，使它既是2的倍数又是3的倍数的概率是.
13. 已知分式 的值为0，那么x的值为 ．14. 如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=5，则这个梯形中位线的长等于 ．
15. 有两块面积相同的小麦试验田，分别收获小麦9000kg和15000kg．已知第一块试验田每公顷的产量比第二块少3000kg，若设第一块试验田每公顷的产量为xkg，根据题意，可得方程 ．
16. 已知⊙O1的半径为3，⊙O2的半径为r，⊙O1与⊙O2只能画出两条不同的公共切线，且O1O2=5，则⊙O2的半径为r的取值范围是 ．
17. 如图所示，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，且∠EAF=80°，则图中阴影部分的面积是 ．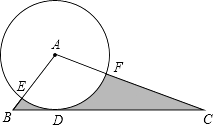
18. 观察下列运算过程：S=1+3+32+33+…+32017+32018 ①，①×3得3S=3+32+33+…+32018+32019 ②，
②﹣①得2S=32019﹣1，S= ．
运用上面计算方法计算：1+5+52+53+…+52018= ．
三、解答题
-
19. Ⅰ．解不等式组 ，并把解集在数轴上表示出来．
Ⅱ．计算：（π﹣3）0+ ﹣2sin45°﹣（ ）﹣1 ．
20. 如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=90º，∠CED=45º，∠DCE=30º，DE= ，BE=2 ．求CD的长和四边形ABCD的面积．
21. 某班同学分三组进行数学活动，对七年级400名同学最喜欢喝的饮料情况，八年级300名同学零花钱的最主要用途情况，九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据．
九年级300名同学完成家庭作业时间情况统计图
时间
1小时左右
1.5小时左右
2小时左右
2.5小时左右
人数
50
80
120
50
根据以上信息，请回答下列问题：
(1)、七年级400名同学中最喜欢喝“冰红茶”的人数是多少；
(2)、补全八年级300名同学中零花钱的最主要用途情况频数分布直方图；(3)、九年级300名同学中完成家庭作业的平均时间大约是多少小时？（结果保留一位小数）
22. 如图所示，在天水至宝鸡（天宝）高速公路建设中需要确定某条隧道AB的长度，已知在离地面2700米高度C处的飞机上，测量人员测得正前方AB两点处的俯角分别是60°和30°，求隧道AB的长．（结果保留根号）
23. 如图，在平面直角坐标系xOy中，函数 （x＞0）的图象与一次函数y=kx－k的图象交点为A（m，2）．
(1)、求一次函数的表达式；
(2)、设一次函数y=kx－k的图象与y轴交于点B，如果P是x轴上一点，且满足△PAB的面积是4，请直接写出P的坐标．
24. 某工程机械厂根据市场需求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22 400万元，但不超过22 500万元，且所筹资金全部用于生产此两型挖掘机，所生产的此两型挖掘机可全部售出，此两型挖掘机的生产成本和售价如下表：型号
A
B
成本（万元/台）
200
240
售价（万元/台）
250
300
(1)、该厂对这两型挖掘机有哪几种生产方案？
(2)、该厂如何生产能获得最大利润？(3)、根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高m万元（m＞0），该厂应该如何生产获得最大利润？（注：利润=售价﹣成本）25. 如图1，已知A（3，0）、B（4，4）、原点O（0，0）在抛物线y=ax2+bx+c （a≠0）上．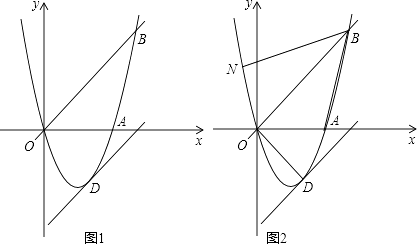
(1)、求抛物线的解析式．
(2)、将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个交点D，求m的值及点D的坐标．(3)、如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P的坐标（点P、O、D分别与点N、O、B对应）26. 如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．
(1)、求直线AB的解析式；
(2)、当点P运动到点（ ，0）时，求此时DP的长及点D的坐标；
(3)、是否存在点P，使△OPD的面积等于 ？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．