重庆市2018届高三文数4月(二诊)调研测试试卷
试卷更新日期:2018-10-12 类型:高考模拟
一、选择题
-
1. 设全集 ,集合 , ,则 ( )A、 B、 C、 D、2. 复数 满足 ,则 ( )A、 B、 C、 D、3. 设等差数列 的前 项和为 ,若 , ,则 ( )A、 B、 C、 D、4. 已知两个非零向量 , 互相垂直,若向量 与 共线,则实数 的值为( )A、 B、 C、 D、5. “ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 执行如图所示的程序框图,如果输入的 ,则输出的 值的取值范围是( )
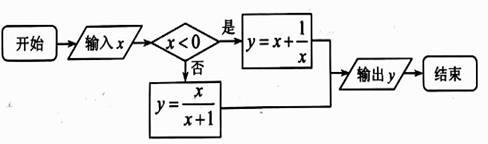 A、 或 B、 C、 或 D、 或7. 曲线 在点 处的切线与两坐标轴所围成的三角形的面积为( )A、 B、 C、 D、8. 已知定义在 上的奇函数 满足 ,且 ,则 的值为( )A、 B、 C、 D、9. 如图,在矩形 中, , ,两个圆的半径都是1,且圆心 , 均在对方的圆周上,在矩形 内随机取一点,则此点取自阴影部分的概率为( )
A、 或 B、 C、 或 D、 或7. 曲线 在点 处的切线与两坐标轴所围成的三角形的面积为( )A、 B、 C、 D、8. 已知定义在 上的奇函数 满足 ,且 ,则 的值为( )A、 B、 C、 D、9. 如图,在矩形 中, , ,两个圆的半径都是1,且圆心 , 均在对方的圆周上,在矩形 内随机取一点,则此点取自阴影部分的概率为( )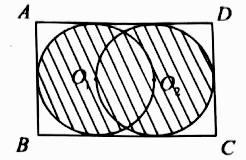 A、 B、 C、 D、10. 设函数 与 的图象在 轴右侧的第一个交点为 ,过点 作 轴的平行线交函数 的图象于点 ,则线段 的长度为( )A、 B、 C、 D、11. 某几何体的三视图如图所示,其正视图为等腰梯形,则该几何体的表面积是( )
A、 B、 C、 D、10. 设函数 与 的图象在 轴右侧的第一个交点为 ,过点 作 轴的平行线交函数 的图象于点 ,则线段 的长度为( )A、 B、 C、 D、11. 某几何体的三视图如图所示,其正视图为等腰梯形,则该几何体的表面积是( )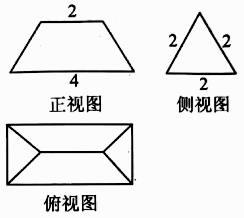 A、 B、 C、 D、12. 设集合 , ,记 ,则点集 所表示的轨迹长度为( )A、 B、 C、 D、
A、 B、 C、 D、12. 设集合 , ,记 ,则点集 所表示的轨迹长度为( )A、 B、 C、 D、二、填空题
-
13. 某公司对一批产品的质量进行检测,现采用系统抽样的方法从100件产品中抽取5件进行检测,对这100件产品随机编号后分成5组,第一组 号,第二组 号,…,第五组 号,若在第二组中抽取的编号为24,则在第四组中抽取的编号为 .14. 已知实数 , 满足 则 的最大值为 .15. 边长为2的等边 的三个顶点 , , 都在以 为球心的球面上,若球 的表面积为 ,则三棱锥 的体积为 .16. 已知双曲线 ( , )的左右焦点分别为 , ,点 在双曲线的左支上, 与双曲线右支交于点 ,若 为等边三角形,则该双曲线的离心率是 .
三、解答题
-
17. 已知数列 的前 项和为 , , .(1)、求 ;(2)、求证: .18. 某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上.社区最近四年内在“文化丹青”上的投资金额统计数据如表:(为了便于计算,把2015年简记为5,其余以此类推)
年份 (年)
5
6
7
8
投资金额 (万元)
15
17
21
27
(附:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘估计分别为 , .)
(1)、利用所给数据,求出投资金额 与年份 之间的回归直线方程 ;(2)、预测该社区在2019年在“文化丹青”上的投资金额.19. 三棱柱 中, , , 分别为棱 , , 的中点.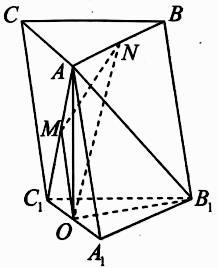 (1)、求证:直线 平面 ;(2)、若三棱柱 的体积为 ,求三棱锥 的体积.20. 如图,已知 , 是椭圆 的左右焦点, 为椭圆 的上顶点,点 在椭圆 上,直线 与 轴的交点为 , 为坐标原点,且 , .
(1)、求证:直线 平面 ;(2)、若三棱柱 的体积为 ,求三棱锥 的体积.20. 如图,已知 , 是椭圆 的左右焦点, 为椭圆 的上顶点,点 在椭圆 上,直线 与 轴的交点为 , 为坐标原点,且 , . (1)、求椭圆 的方程;(2)、过点 作两条互相垂直的直线分别与椭圆 交于 , 两点(异于点 ),证明:直线 过定点,并求该定点的坐标.
(1)、求椭圆 的方程;(2)、过点 作两条互相垂直的直线分别与椭圆 交于 , 两点(异于点 ),证明:直线 过定点,并求该定点的坐标.