新疆维吾尔自治区2018届高三理数第二次适应性检测试卷
试卷更新日期:2018-10-12 类型:高考模拟
一、选择题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 为实数 为实数,则 =( )A、 B、 C、1 D、3. 已知 、 、 三点不共线,且点 满足 ,则下列结论正确的是( )A、 B、 C、 D、4. 若函数 的图像向右平移 个单位后所得的函数为奇函数,则 的最小值为( )A、 B、 C、 D、5. 参加2018年自治区第一次诊断性测试的10万名理科考生的数学成绩 近似地服从正态分布 ,估计这些考生成绩落在 的人数为( )
(附: ,则 )
A、311740 B、27180 C、13590 D、45606. 某空间几何体的三视图如图所示,则该几何体的外接球的体积为( )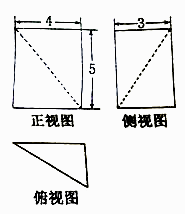 A、 B、 C、 D、7. 在 中,“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件8. 已知实数 , 满足 ,则使不等式 恒成立的实数 的取值集合是( )A、 B、 C、 D、9. 图中的程序框图所描述的算法称为欧几里得辗转相除法,若输入 , 则输出的 的值为( )
A、 B、 C、 D、7. 在 中,“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件8. 已知实数 , 满足 ,则使不等式 恒成立的实数 的取值集合是( )A、 B、 C、 D、9. 图中的程序框图所描述的算法称为欧几里得辗转相除法,若输入 , 则输出的 的值为( )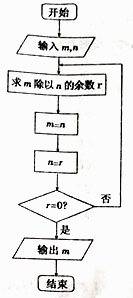 A、5 B、25 C、45 D、3510. 已知点 在幂函数 的图象上,设 ,则 的大小关系为( )A、 B、 C、 D、11. 若 展开式中含 项的系数为-80,则 等于( )A、5 B、6 C、7 D、812. 若抛物线 的焦点为 ,其准线经过双曲线 的左焦点,点 为这两条曲线的一个交点,且 ,则双曲线的离心率为( )A、 B、 C、 D、
A、5 B、25 C、45 D、3510. 已知点 在幂函数 的图象上,设 ,则 的大小关系为( )A、 B、 C、 D、11. 若 展开式中含 项的系数为-80,则 等于( )A、5 B、6 C、7 D、812. 若抛物线 的焦点为 ,其准线经过双曲线 的左焦点,点 为这两条曲线的一个交点,且 ,则双曲线的离心率为( )A、 B、 C、 D、二、填空题
-
13. 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图.为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在 (元)月收入段应抽出人.
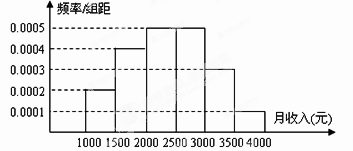 14. 在直线 , , , 围成的区域内撒一粒豆子,则落入 , , 围成的区域内的概率为 .15. 在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是 .16. 设函数 ,其中 表示不超过 的最大整数,如 , , ,若直线 ( )与函数 的图象恰好有两个不同的交点,则 的取值范围是 .
14. 在直线 , , , 围成的区域内撒一粒豆子,则落入 , , 围成的区域内的概率为 .15. 在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是 .16. 设函数 ,其中 表示不超过 的最大整数,如 , , ,若直线 ( )与函数 的图象恰好有两个不同的交点,则 的取值范围是 .三、解答题
-
17. 在等差数列 中,已知 , .
(I)求数列 的通项 ;
(II)若 ,求数列 的前 项和 .
18. 如图,在斜三棱柱 中,侧面 与侧面 都是菱形, , .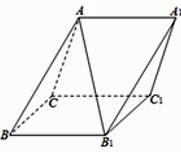
(Ⅰ)求证: ;
(Ⅱ)若 ,求平面 与平面 所成的锐二面角的余弦值.
19. 甲乙两名运动员互不影响地进行四次设计训练,根据以往的数据统计,他们设计成绩均不低于8环(成绩环数以整数计),且甲乙射击成绩(环数)的分布列如下:

(I)求 , 的值;
(II)若甲乙两射手各射击两次,求四次射击中恰有三次命中9环的概率;
(III)若两个射手各射击1次,记两人所得环数的差的绝对值为 ,求 的分布列和数学期望.
20. 已知动点 是圆 : 上的任意一点,点 与点 的连线段的垂直平分线和 相交于点 .(I)求点 的轨迹 方程;
(II)过坐标原点 的直线 交轨迹 于点 , 两点,直线 与坐标轴不重合. 是轨迹 上的一点,若 的面积是4,试问直线 , 的斜率之积是否为定值,若是,求出此定值,否则,说明理由.