吉林省延边州2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2018-10-11 类型:期末考试
一、单选题
-
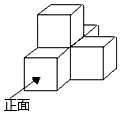
1. 若等式(﹣5)□5=0成立,则□内的运算符号为( )A、+ B、﹣ C、× D、÷2. 如图是由五个相同的小正方体组成的立体图形,从上面看到的图形是( )
 A、
A、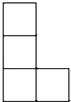 B、
B、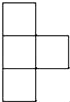 C、
C、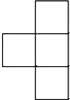 D、
D、 3. 下列运算,结果正确的是( )A、a+2a2=3a3 B、2a+b=2ab C、4a﹣a=3 D、3a2b﹣2ba2=a2b4. 已知x=y,则下列各式中,不一定成立的是( )A、x﹣2=y﹣2 B、 C、﹣3x=﹣3y D、5. 已知关于x的方程(m﹣2)x|m﹣1|﹣3=0是一元一次方程,则m的值是( )A、2 B、0 C、1 D、0或26. 一项工程甲单独做需20天完成,乙单独做需30天完成,甲先单独做4天,然后甲、乙两人合作x天完成这项工程,则下面所列方程正确的是( )A、 B、 C、 D、
3. 下列运算,结果正确的是( )A、a+2a2=3a3 B、2a+b=2ab C、4a﹣a=3 D、3a2b﹣2ba2=a2b4. 已知x=y,则下列各式中,不一定成立的是( )A、x﹣2=y﹣2 B、 C、﹣3x=﹣3y D、5. 已知关于x的方程(m﹣2)x|m﹣1|﹣3=0是一元一次方程,则m的值是( )A、2 B、0 C、1 D、0或26. 一项工程甲单独做需20天完成,乙单独做需30天完成,甲先单独做4天,然后甲、乙两人合作x天完成这项工程,则下面所列方程正确的是( )A、 B、 C、 D、二、填空题
-
7. 火星和地球的最近距离约为55000000千米,用科学记数法表示55000000的结果是千米.8. 苹果进价是每千克x元,要得到10%的利润,则该苹果售价应是每千克元(用含x的代数式表示)9. 若整式xn﹣2﹣5x+2是关于x的三次三项式,那么n= .10. 若单项式 ax2yn+1与﹣ axmy4的差仍是单项式,则m﹣2n= .11. 若a-2b=3,则9-2a+4b的值为 .12. 如图所示,OA表示偏28°方向,射线OB表示方向,∠AOB= .
 13. 已知线段AB,在AB的延长线上取一点C,使AC=2BC,在AB的反向延长线上取一点D,使DA=2AB,那么线段AC:DB= .
13. 已知线段AB,在AB的延长线上取一点C,使AC=2BC,在AB的反向延长线上取一点D,使DA=2AB,那么线段AC:DB= .
14. 观察下面的一列单项式:2x2 , 4x3 , 8x4 , …,根据你发现的规律,写出第n个单项式为 . (n为正整数)三、解答题
-
15. 计算: .16. .17. 解下列方程:2(x﹣1)﹣3(x+2)=12.18. .19. 先化简,再求值. ,其中a=﹣1,b= .20. 如图,平面上有四个点A,B,C,D,根据下列语句画图:
 (1)、画线段AC、BD交于E点;(2)、作射线BC;(3)、取一点P,使点P既在直线AB上又在直线CD上.
(1)、画线段AC、BD交于E点;(2)、作射线BC;(3)、取一点P,使点P既在直线AB上又在直线CD上.
21. 一个角的余角比它的补角的 还少40°,求这个角的度数.22. 如图所示,池塘边有块长为20m,宽为10m的长方形土地,现在将其余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用含x的式子表示: (1)、菜地的长a=m,菜地的宽b=m;菜地的周长C=m;(2)、求当x=1m时,菜地的周长C.23. 已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.(1)、求k的值;(2)、在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.24. 小刚和小强从A、B两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后2h两人相遇,相遇时小刚比小强多行进24km,相遇后0.5h小刚到达B地,两人的行进速度分别是多少?相遇后经过多少时间小强到达A地?25. 直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)、菜地的长a=m,菜地的宽b=m;菜地的周长C=m;(2)、求当x=1m时,菜地的周长C.23. 已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.(1)、求k的值;(2)、在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.24. 小刚和小强从A、B两地同时出发,小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出发后2h两人相遇,相遇时小刚比小强多行进24km,相遇后0.5h小刚到达B地,两人的行进速度分别是多少?相遇后经过多少时间小强到达A地?25. 直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.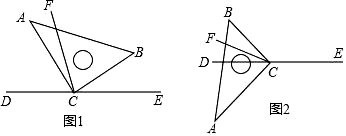 (1)、在图1中,若∠BCE=40°,求∠ACF的度数;(2)、在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);(3)、将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.26. 新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
(1)、在图1中,若∠BCE=40°,求∠ACF的度数;(2)、在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);(3)、将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.26. 新学期开学,某体育用品商店开展促销活动,有两种优惠方案.方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)、求该商店销售的乒乓球拍每副的标价.(2)、如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.