河北省鸡泽、曲周、邱县、馆陶四县2017-2018学年高二下学期文数期末联考试卷
试卷更新日期:2018-10-10 类型:期末考试
一、单选题
-
1. 设全集 ,则 ( )A、 B、 C、 D、2. 已知复数 满足 ,则 ( )A、 B、 C、 D、3. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数 的零点所在的一个区间是( )A、 B、 C、 D、5. 若 满足 ,则 的最大值为( )A、 B、3 C、 D、46. 已知 ,则 ( )A、 B、 C、 D、7. 已知函数 ,下列结论错误的是( )A、 的最小正周期为 B、 在区间 上是增函数 C、 的图象关于点 对称 D、 的图象关于直线 对称8. 某三棱锥的三视图如图所示,则其体积为( )
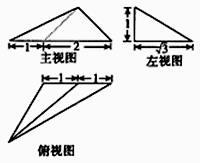 A、 B、 C、 D、9. 如图中的程序框图表示求三个实数 中最大数的算法,那么在空白的判断框中,应该填入( )
A、 B、 C、 D、9. 如图中的程序框图表示求三个实数 中最大数的算法,那么在空白的判断框中,应该填入( )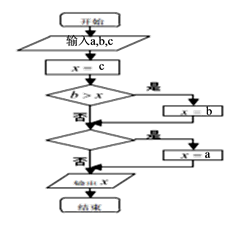 A、 B、 C、 D、10. 边长为 的两个等边 所在的平面互相垂直,则四面体 的外接球的表面积为( )A、 B、 C、 D、11. 已知抛物线 的焦点到双曲线 的一条渐近线的距离为 ,则该双曲线的离心率为( )A、 B、 C、 D、12. 已知方程 有4个不同的实数根,则实数 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 边长为 的两个等边 所在的平面互相垂直,则四面体 的外接球的表面积为( )A、 B、 C、 D、11. 已知抛物线 的焦点到双曲线 的一条渐近线的距离为 ,则该双曲线的离心率为( )A、 B、 C、 D、12. 已知方程 有4个不同的实数根,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 某单位有420名职工,现采用系统抽样方法抽取21人做问卷调查,将420人按1,2,…,420随机编号,则抽取的21人中,编号落入区间 的人数为.14. 在 中, 是边 的中点,则 .15. 若点 在直线 上,则 的最小值是.16. 在 中,角 所对的边分别为 ,则 .
三、解答题
-
17. 已知数列 是等比数列,其前 项和为 ,满足 .(1)、求数列 的通项公式;(2)、是否存在正整数 ,使得 ?若存在,求出符合条件的 的最小值;若不存在,说明理由.18. 某校为了解本校学生在校小卖部的月消费情况,随机抽取了60名学生进行统计.得到如下样本频数分布表:
月消费金额(单位:元)
人数
30
6
9
10
3
2
记月消费金额不低于300元为“高消费”,已知在样本中随机抽取1人,抽到是男生“高消费”的概率为 .
下面的临界值表仅供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式: ,其中 ,其中)
(1)、从月消费金额不低于400元的学生中随机抽取2人,求至少有1人月消费金额不低于500元的概率;(2)、请将下面的 列联表补充完整,并判断是否有 的把握认为“高消费”与“男女性别”有关,说明理由.高消费
非高消费
合计
男生
女生
25
合计
60
19. 如图,四边形 为梯形, 平面 , ,为 中点.
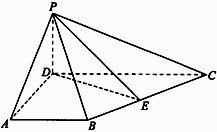 (1)、求证:平面 平面 ;(2)、线段 上是否存在一点 ,使 平面 ?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.20. 已知椭圆 的离心率为 ,椭圆 与 轴交于 两点,且 .(1)、求椭圆 的方程;(2)、设点 是椭圆 上的一个动点,且直线 与直线 分别交于 两点.是否存在点 使得以 为直径的圆经过点 ?若存在,求出点 的横坐标;若不存在,说明理由.
(1)、求证:平面 平面 ;(2)、线段 上是否存在一点 ,使 平面 ?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.20. 已知椭圆 的离心率为 ,椭圆 与 轴交于 两点,且 .(1)、求椭圆 的方程;(2)、设点 是椭圆 上的一个动点,且直线 与直线 分别交于 两点.是否存在点 使得以 为直径的圆经过点 ?若存在,求出点 的横坐标;若不存在,说明理由.