2018-2019学年数学浙教版九年级上册第3章 圆的基本性质单元检测b卷
试卷更新日期:2018-10-10 类型:单元试卷
一、选择题
-
1. 如图,AB是⊙O的直径,点D,C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC的度数为( )
 A、15° B、30° C、45° D、60°2. 如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )
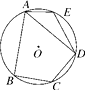
A、15° B、30° C、45° D、60°2. 如图,⊙O△ABC的三条边所得的弦长相等,则下列说法正确的是( )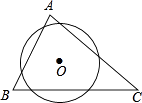 A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形3. 如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A、点O是△ABC的内心 B、点O是△ABC的外心 C、△ABC是正三角形 D、△ABC是等腰三角形3. 如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( ) A、3 B、4 C、3 D、44. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A、3 B、4 C、3 D、44. 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( ) A、弦AB的长等于圆内接正六边形的边长 B、弦AC的长等于圆内接正十二边形的边长 C、AC=BC D、∠BAC=30°5. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10.上述结论中正确的个数是( )
A、弦AB的长等于圆内接正六边形的边长 B、弦AC的长等于圆内接正十二边形的边长 C、AC=BC D、∠BAC=30°5. 如图,在⊙O中,AB是⊙O的直径,AB=10, ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10.上述结论中正确的个数是( ) A、1 B、2 C、3 D、46. 已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )
A、1 B、2 C、3 D、46. 已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为( )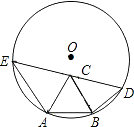 A、 B、1 C、 D、a7. 如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度.
A、 B、1 C、 D、a7. 如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB的度数为( )度. A、30 B、45 C、50 D、608. 一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
A、30 B、45 C、50 D、608. 一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( ) A、 m B、 m C、 m D、 m9.
A、 m B、 m C、 m D、 m9.如图,四边形BDCE内接于以BC为直径的⊙A,已知:BC=10,cos∠BCD= , ∠BCE=30°,则线段DE的长是( )
 A、 B、7 C、4+3 D、3+410. 如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为何?( )
A、 B、7 C、4+3 D、3+410. 如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为何?( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,AB是⊙O的直径,∠C=20°,则∠BOC的度数是 .
 12. 如图,点D是等腰 的底边AB上的点,若 且 ,将 绕点C逆时针旋转,使它与 重合,则 度
12. 如图,点D是等腰 的底边AB上的点,若 且 ,将 绕点C逆时针旋转,使它与 重合,则 度 13. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 .
13. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为7,则GE+FH的最大值为 . 14. 如图,P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,若x、y都是整数,则这样的点共有个.
14. 如图,P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,若x、y都是整数,则这样的点共有个. 15. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
15. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 . 16. 如图所示,AB是半圆的直径,∠C的两边分别与半圆相切于A、D两点,DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分的面积为 .
16. 如图所示,AB是半圆的直径,∠C的两边分别与半圆相切于A、D两点,DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分的面积为 .
三、解答题
-
17. 如图,已知点O为等腰三角形ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.

求证:
(1)、∠AOE=∠BOD;
(2)、 .18. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. (1)、若∠CBD=39°,求∠BAD的度数;(2)、求证:∠1=∠2.19. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
(1)、若∠CBD=39°,求∠BAD的度数;(2)、求证:∠1=∠2.19. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE. (1)、求∠ACB的度数;
(1)、求∠ACB的度数;
(2)、过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
20. 如图,已知 中, ,把 绕A点沿顺时针方向旋转得到 ,连接BD,CE交于点F. (1)、求证: ≌ ;
(1)、求证: ≌ ;
(2)、若 , ,当四边形ADFC是菱形时,求BF的长.
21. 如图,已知AB为⊙O的直径,CD是弦,且AB CD于点E。连接AC、OC、BC。 (1)、求证: ACO= BCD。
(1)、求证: ACO= BCD。
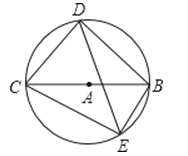
(2)、若EB= ,CD= ,求⊙O的直径。22. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OB,OC,AC,OB与AC相交于点E. (1)、求∠OCA的度数;
(1)、求∠OCA的度数;
(2)、若∠COB=3∠AOB,OC=2 ,求图中阴影部分的面积(结果保留π和根号).