2018-2019学年数学浙教版九年级上册3.8 弧长及扇形的面积（2）同步练习

试卷更新日期：2018-10-10 类型：同步测试

进入出卷网下载

一、选择题

1. 右图是某商品的标志图案，AC与BD是⊙O的两条直径，首尾顺次连接点A、B、C、D，得到四边形ABCD．若AC＝10cm，∠BAC＝36°，则图中阴影部分的面积为（）

A、5πcm² B、10πcm² C、15πcm² D、20πcm²

查看试题解析
2. 如图，在半径为2，圆心角为90°的扇形内，以BC为直径作半圆交AB于点D，连接CD，则阴影部分的面积是（）

A、 $\frac{1}{2} π - 1$ B、 $\frac{1}{2} π - 2$ C、 $π - 2$ D、 $π - 1$

查看试题解析
3. 如图，一张半径为1的圆形纸片在边长为 $a (a \geq 3)$ 的正方形内任意移动，则在该正方形内，这张圆形纸片“不能接触到的部分”的面积是（）

A、 $a^{2} - π$ B、4－π C、π D、 $(4 - π) a^{2}$

查看试题解析
4. 如图，线段 $A B = 2$ ，分别以A，B为圆心，以AB的长为半径作弧，两弧交于C，D两点，则阴影部分的面积为（）

A、 $\frac{2}{3} π - 4 \sqrt{3}$ B、 $\frac{4}{3} π - 4 \sqrt{3}$ C、 $\frac{2}{3} π + 4 \sqrt{3}$ D、 $\frac{4}{3} π + 4 \sqrt{3}$

查看试题解析
5. 如图，正方形ABCD的边长为2cm，以点B为圆心，AB的长为半径作弧AC，则图中阴影部分的面积为（）

A、(4－π)cm² B、(8－π)cm² C、(2π－4)cm² D、(π－2)cm²

查看试题解析
6. 如图，在四边形ABCD中，AB=CD，AD∥BC，以点B为圆心，BA为半径的圆弧与BC交于点E，四边形AECD是平行四边形，AB=3，则弧AE 的弧长为（）

A、 $\frac{1}{2}$ π B、π C、 $\frac{3}{2}$ π D、3

查看试题解析
7. 如图，在△ABC中，∠C=90°，AC=BC，AB=2 $\sqrt{2}$ ，点O为AB的中点，以点O为圆心作半圆与边AC相切于点D．则图中阴影部分的面积为（）

A、1﹣ $\frac{1}{4}$ π B、1﹣ $\frac{1}{2}$ π C、2﹣ $\frac{3}{4}$ π D、2﹣ $\frac{1}{4}$ π

查看试题解析
8. 如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD=12，AD：AB=1：2，则图中阴影部分的面积为（）

A、12 $\sqrt{3}$ B、 $15 \sqrt{3} - 6 π$ C、 $30 \sqrt{3} - 12 π$ D、 $48 \sqrt{3} - 36 π$

查看试题解析
9. 如图，边长为1的正方形ABCD绕点A逆时针旋转 $45 °$ 后得到正方形 $A B_{1} C_{1} D_{1}$ ，边 $B_{1} C_{1}$ 与CD交于点O，则图中阴影部分的面积是（）

A、 $\frac{π}{4} - 2 - \sqrt{2}$ B、 $\frac{π}{4} - 2 + \sqrt{2}$ C、 $\frac{π}{4} + \frac{1}{2}$ D、 $\frac{π}{4} - \frac{1}{2}$

查看试题解析

二、填空题

10. 如图，在矩形ABCD中，以AD为直径的半圆与边BC相切于点E，若AD=4，则图中的阴影部分的面积为.

查看试题解析
11. 如图，在扇形AOB中， $∠ A O B = 90 °$ ， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ，过点C作 $C D ⊥ O B$ 于点D，以CD为边向右作正方形CDEF，若 $O A = \sqrt{2}$ ，则阴影部分的面积是 $(结果保留 π)$

查看试题解析
12. 如图是圆心角为 30°，半径分别是 1、3、5、7、…的扇形组成的图形，阴影部分的面积依次记为 S1、S2、S3、…，则 S3= ， Sn=.结果保留 π）

查看试题解析
13. 如图，将半径为2，圆心角为 120° 的扇形OAB绕点A逆时针旋转 60° ，点O，B的对应点分别为 O′，B′，连接 BB′，则图中阴影部分的面积是．

查看试题解析
14. 如图，在 $△ A B C$ 中， $CA=CB=4$ ， $∠ ACB=90 °$ ，以AB中点D为圆心，作圆心角为 $90 °$ 的扇形DEF，点C恰好在弧EF上，则图中阴影部分面积为．

查看试题解析
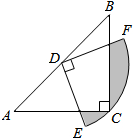15. 如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）

查看试题解析
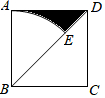16. 如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA=2，AC=1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是（1， $\sqrt{3}$ ），则在旋转过程中线段OC扫过部分（阴影部分）的面积为．

查看试题解析

三、解答题

17. 如图所示，正方形ABCD的边长为1，点E为AB的中点，以E为圆心，1为半径作圆，分别交AD，BC于M，N两点，与DC切于点P，则图中阴影部分面积是．

查看试题解析
18. 如图，AB是⊙O的弦，半径OA=20cm，∠AOB=120^o ．求：

(1)、△OAB的面积．

(2)、阴影部分的面积．（精确到1cm²）

查看试题解析
19. 如图，AB为 $⊙ O$ 的直径，AB=AC，BC交 $⊙ O$ 于点D，AC交 $⊙ O$ 于点E．

(1)、求证：BD=CD；

(2)、若AB=8，∠BAC=45°，求阴影部分的面积．

查看试题解析
20. 如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E，弧 $C D =弧 C E$ .

(1)、求证：OA＝OB；

(2)、已知AB＝4 $\sqrt{3}$ ，OA＝4，求阴影部分的面积．

查看试题解析
21. 如图，一个横截面为Rt△ABC的物体，∠ACB=90°，∠CAB=30°，BC=1m，工人师傅要把此物体搬到墙边，先将AB边放在地面（直线l）上，再按顺时针方向绕点B翻转到△A₁BC₁的位置（BC₁在l上），最后沿射线BC₁的方向平移到△A₂B₂C₂的位置，其平移的距离为线段AC的长度（此时A₂C₂恰好靠在墙边）．

(1)、请直接写出AB= ， AC=；

(2)、画出在搬动此物体的整个过程中A点所经过的路径，并求出该路径的长度．

(3)、设O、H分别为边AB、AC的中点，在将△ABC绕点B顺时针方向翻转到△A₁BC₁的位置这一过程中，求线段OH所扫过部分的面积．

查看试题解析
22. 如图，O是 $△ A B C$ 的内心，BO的延长线和 $△ A B C$ 的外接圆相交于D，连结DC、DA、OA、OC，四边形OADC为平行四边形．

(1)、求证： $△ B O C$ ≌ $△ C D A$ ．

(2)、若 $A B = 3$ ，求阴影部分的面积．

查看试题解析

2018-2019学年数学浙教版九年级上册3.8 弧长及扇形的面积（2） 同步练习

一、选择题

二、填空题

三、解答题

2018-2019学年数学浙教版九年级上册3.8 弧长及扇形的面积（2）同步练习