2018-2019学年数学浙教版九年级上册3.7 正多边形 同步练习
试卷更新日期:2018-10-10 类型:同步测试
一、选择题
-
1. 一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A、r= R B、r= R C、r= R D、r= R2. 半径为r的圆的内接正三角形的边长是( )A、2r B、 C、 D、3. 正三角形的边心距、半径和高的比是( )A、1:2:3 B、1: : C、1: :3 D、1:2:4. 如图,以正五边形ABCDE的对角线AC为边作正方形ACFG,使点B落在正方形ACFG外,则∠EAG的大小为( ) A、 B、 C、 D、5. 如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子( )
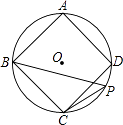
A、 B、 C、 D、5. 如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子( )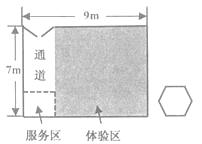 A、4张 B、5张 C、6张 D、7张6. 如图,正五边形ABCDE的顶点A在y轴上,边CD∥x轴,若点E坐标为(3,2),则点B的坐标为( )
A、4张 B、5张 C、6张 D、7张6. 如图,正五边形ABCDE的顶点A在y轴上,边CD∥x轴,若点E坐标为(3,2),则点B的坐标为( ) A、(3,-2) B、(-3,2) C、(-3,-2) D、(2,3)7. 如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
A、(3,-2) B、(-3,2) C、(-3,-2) D、(2,3)7. 如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( ) A、36° B、42° C、45° D、48°8. 如图,在正八边形ABCDEFGH中,连接AC,AE,则 的值是( )
A、36° B、42° C、45° D、48°8. 如图,在正八边形ABCDEFGH中,连接AC,AE,则 的值是( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
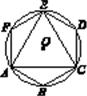
9. 已知正方形的边长为2cm,那么它外接圆的半径长是cm.10. 圆内接正六边形的边长为10cm,则它的边心距等于cm.11. 如图所示的正六边形 ABCDEF,连结 FD,则∠FDC 的大小为 .
 12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=.
12. 如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM=.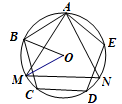 13. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .
13. 如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为 .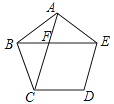 14. 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为 .
14. 如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为 .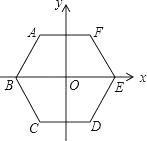 15. 如图,正六边形ABCDEF的边长是6+4 ,点O1 , O2分别是△ABF,△CDE的内心,则O1O2= .
15. 如图,正六边形ABCDEF的边长是6+4 ,点O1 , O2分别是△ABF,△CDE的内心,则O1O2= .
三、解答题
-
16. 如图,正三角形ABC内接于⊙O,若AB= cm,求⊙O的半径.
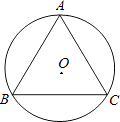 17. 如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.
17. 如图,正六边形ABCDEF内接于⊙O,若⊙O的内接正三角形ACE的面积为48 ,试求正六边形的周长.