2018-2019学年数学浙教版九年级上册3.5 圆周角（2） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 如图，BD是⊙O的直径，∠CBD=30°，则∠A的度数为（ ）
A、30° B、45° C、60° D、75°2. 如图，在⊙O中，直径CD⊥弦AB，若∠C=30°，则∠BOD的度数是（ ）
A、30° B、40° C、50° D、60°3. 如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB=110°，则∠AED的度数为（ ）
A、15° B、20° C、25° D、30°4. 如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（ ）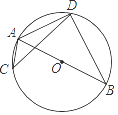
A、∠ADC B、∠ABD C、∠BAC D、∠BAD5. 如图，OA，OC是⊙O的半径，点B在⊙O上，若AB∥OC，∠BCO=21°，则∠AOC的度数是（ ）
A、42° B、21° C、84° D、60°6. 如图，AB是⊙O的直径，CD是弦，且AB∥CD，若AB=8，∠ABC=30°，则弦AD的长为（ ）
A、 B、 C、 D、87. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，已知DE＝6，∠BAC＋∠EAD＝180°，则弦BC的长等于（ ）
A、 B、 C、8 D、68. 如图，A，B，C，D是⊙O上的四个点，B是弧AC的中点，M是半径OD上任意一点．若∠BDC=40°，则∠AMB的度数不可能是（ ）
A、45° B、60° C、75° D、85°二、填空题
-
9. 如图，点A，B，C，D分别在⊙O上， ，若∠AOB=40°，则∠ADC的大小是度．
10. 如图，AB为△ADC的外接圆⊙O的直径，若∠BAD=50°，则∠ACD=°．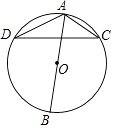
11. 如图，点A、B、C都在⊙O上，OC⊥OB，点A在劣弧BC上，且OA=AB，则∠ABC= ．
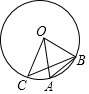12. 如图，已知AB是⊙O的直径，∠D=42°，则∠CAB的度数为 ．
13. ⊙O是等边三角形ABC的外接圆，点D是⊙O上一点，则∠BDC =；
14. 如图，BC为⊙O的弦，OA⊥BC交⊙O于点A，∠AOB=70°，则∠ADC= ．
15. 如图，⊙O是△ABC的外接圆，AO⊥BC于点F，D为 的中点，且 的度数为70°则∠BAF=度
三、解答题
-
16. 如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．
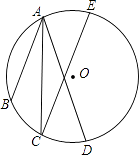17. 如图，CD为⊙O直径，以C点为圆心，CO为半径作弧，交⊙O于A、B两点，求证：AD=BD=BA．
18. 如图，在⊙O中， ，∠ACB=60°，求证∠AOB=∠BOC=∠COA.
19. 如图，△ABC中，AB＝AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD，DE.
(1)、求证：D是BC的中点；
(2)、若DE＝3，BD－AD＝2，求⊙O的半径．20. 如图，点B，C为⊙O上一动点，过点B作BE∥AC，交⊙O于点E，点D为射线BC上一动点，且AC平分∠BAD，连接CE．
(1)、求证：AD∥EC；
(2)、连接EA，若BC=6，则当CD=时，四边形EBCA是矩形．
