2018-2019学年数学浙教版九年级上册3.5 圆周角（1）同步练习

试卷更新日期：2018-10-10 类型：同步测试

进入出卷网下载

1. 如图，⊙O中，半径OC⊥弦AB于点D，点E在⊙O上，∠E=22.5°，AB=4，则半径OB等于（）

A、 $\sqrt{2}$ B、2 C、2 $\sqrt{2}$ D、3

查看试题解析
2. 如图，已知圆周角 $∠ A C B = 130^{\circ}$ ，则圆心角 $∠ A O B$ =（）

A、130° B、115° C、100° D、50°

查看试题解析
3. 如图，AB是 $⊙ O$ 的直径，CD是 $⊙ O$ 的弦，连结AC，AD，BD，若 $∠ C A B = 35 °$ ，则 $∠ A D C$ 的度数为（）

A、 $35 °$ B、 $55 °$ C、 $65 °$ D、 $70 °$

查看试题解析
4. 如图，AB是 $⊙ O$ 的直径，C，D为 $⊙ O$ 上的两点，若 $A B = 6$ ， $B C = 3$ ，则 $∠ B D C$ 的大小是（）

A、 $60^{\circ}$ B、 $45^{\circ}$ C、 $30^{\circ}$ D、 $15^{\circ}$

查看试题解析
5. 如图， $△ A B C$ 内接于 $⊙ O$ ， $∠ A B C = 71 °$ ， $∠ C A B = 53 °$ ，点D在AC弧上，则 $∠ A D B$ 的大小为（）

A、 $46^{\circ}$ B、 $53^{\circ}$ C、 $56^{\circ}$ D、 $71^{\circ}$

查看试题解析
6. 如图， $⊙ O$ 的直径CD过弦EF的中点G， $∠ D C F = 20 °$ ，则 $∠ D O E$ 等于（）

A、 $10 °$ B、 $20 °$ C、 $40 °$ D、 $80 °$

查看试题解析
7. 如图，⊙O中，OA⊥BC，∠AOC=50°，则∠ADB的度数为（）

A、15° B、25° C、30° D、50°

查看试题解析
8. 如图，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠A=60°，∠ADC=85°，则∠C的度数是（）

A、25° B、27.5° C、30° D、35°

查看试题解析

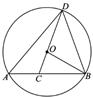
15. 如图，已知AB是⊙O的弦，OB=4，∠OBC=30°，点C是弦AB上任意一点(不与A，B重合)，连接CO并延长CO交⊙O于点D，连接AD、DB.当∠ADC=18°时，求∠DOB的度数.

查看试题解析
16. 如图，⊙O是△ABC的外接圆，∠A＝45°，BD是直径，BD＝2，连接CD，求BC的长．

查看试题解析
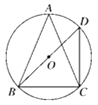17. 如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB于点E，BD交CE于点F.
求证：CF＝BF.

查看试题解析
18. 如图， $A B$ 是⊙O的一条弦， $O D ⊥ A B$ ，垂足为 $C$ ，交⊙O于点D，点 $E$ 在⊙O上。

(1)、若 $∠ A O D = 52^{\circ}$ ，求 $∠ D E B$ 的度数；

(2)、若 $O C = 3$ ， $O A = 5$ ，求 $A B$ 的长。

查看试题解析
19. 如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．

(1)、若∠AOD＝52°，求∠DEB的度数；

(2)、若CD＝2，BA＝8，求半径的长．

查看试题解析
20. 如图， $⊙ O$ 的直径AB的长为10，弦AC的长为 $5 ， ∠ A C B$ 的平分线交 $⊙ O$ 于点D．

(1)、求BC的长；

(2)、求弦BD的长．

查看试题解析

2018-2019学年数学浙教版九年级上册3.5 圆周角（1） 同步练习