2018-2019学年数学浙教版九年级上册3.4 圆心角（2） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 如果两条弦相等，那么（ ）A、这两条弦所对的圆心角相等 B、这两条弦所对的弧相等 C、这两条弦所对的弦心距相等 D、以上说法都不对2. 已知⊙O的半径是10cm， 是120°，那么弦AB的弦心距是（ ）
A、5cm B、 cm C、 cm D、 cm3. 如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，若DE=6，∠BAC+∠EAD=180°，则弦BC的长等于（ ）
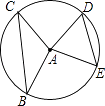A、8 B、10 C、11 D、124. 如图，已知AB和CD是⊙O的两条等弦．OM⊥AB，ON⊥CD，垂足分别为点M、N，BA、DC的延长线交于点P，联结OP．下列四个说法中：①弧AB=弧CD；②OM=ON；③PA=PC；④∠BPO=∠DPO，正确的个数是（ ）
A、1 B、2 C、3 D、45. 下列说法中正确的是（ ）①圆心角是顶点在圆心的角；②两个圆心角相等，它们所对的弦相等；③两条弦相等，圆心到这两弦的距离相等；④在等圆中，圆心角不变，所对的弦也不变．
A、①③ B、②④ C、①④ D、②③6.如图，MN是⊙O的直径，MN=8，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为（ ）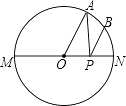
A、 B、2 C、3 D、47. 如图，已知 的半径为5，AB⊥CD，垂足为P，且AB=CD=8，则OP的长为（ ）
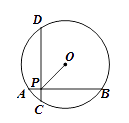A、3 B、4 C、 D、二、填空题
-
8. 如图，已知AB，CD是⊙O的两条弦，OE，OF分别为AB，CD的弦心距，连接OA，OB，OC，OD，如果AB＝CD，则可得出结论： ． (至少填写两个)
9. 如图，半径为5的⊙O中，弦AB，CD所对的圆心角分别是∠A0B，∠C0D．已知CD=6，∠A0B +∠C0D=180°，则弦AB的弦心距等于 ．
10. 如图，在⊙O中，C，D分别是OA，OB的中点，MC⊥AB，ND⊥AB，M，N在⊙O上．下列结论：①MC＝ND；② ；③四边形MCDN是正方形；④MN＝ AB，其中正确的结论是(填序号)．
三、解答题
-
11. 如图，已知AB、CD是⊙O的两条弦，OE⊥AB于E，OF⊥CD于F，OE=OF，求证：AB=CD．
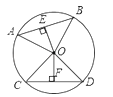12. 如图，在⊙O中，C、D是直径AB上两点，且AC=BD，MC⊥AB，ND⊥AB，M、N在⊙O上，求证： .
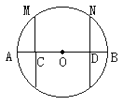13. 如图，在⊙ 中， ， ，ＯC分别交AC，BD于E、F，求证：
14. 如图，四边形ABCD内接于⊙O，AC和BD是对角线，AB＝CD.
求证：
(1)、AC＝DB；(2)、AD∥BC15. 如图， 的半径为5，弦 于E， ．
(1)、求证： ；(2)、若 于F， 于G，试说明四边形OFEG是正方形．16. 我们学习了“圆心角、弧、弦的关系”，实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距(弦心距指从圆心到弦的距离，如图1中的OC、OC′，弦心距也可以说成圆心到弦的垂线段的长度)中有一组量相等，那么它们对应的其余各组量也相等．请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题：如图2，O是∠EPF的平分线上一点，以点O为圆心的圆与角的两边分别交于点A、B、C、D．
(1)、求证：AB＝CD；(2)、若角的顶点P在圆上，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明．17. 如图，⊙O的两条弦AB、CD交于点E，OE平分∠BED．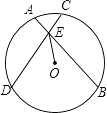
(1)、求证：AB=CD；(2)、若∠BED=60°，EO=2，求DE﹣AE的值．