2018-2019学年数学浙教版九年级上册3.3 垂径定理（2） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 下列命题：（1）垂直于弦的直线平分弦；（2）平分弦的直径必垂直于弦，并且平分弦所对的两条弧；（3）平分弦的直线必过圆心；（4）弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有（ )A、1个 B、2个 C、3个 D、4个2. 垂径定理及推论中的四条性质：①经过圆心；②垂直于弦；③平分弦；④平分弦所对的弧．由上述四条性质组成的命题中，其中是假命题的是（ ）A、①②⇒③④ B、①③⇒②④ C、①④⇒②③ D、②③⇒①④3. 如图，CD是⊙O的直径，弦AB⊥CD于点E，连接BC，BD，下列结论中不一定正确的是（ ）
A、AE＝BE B、 C、OE＝DE D、∠DBC＝90°4. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16cm，则球的半径为（ ）
A、10 cm B、10cm C、10 cm D、8 cm5. 如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D，过点C作⊙O切线交OE的延长线于点F，已知BC=8，DE=2，则⊙O的半径为（ ）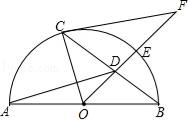
A、8 B、5 C、2.5 D、66. 如图，在△ABC中，AB＝AC，D是边BC的中点，一个圆过点A，交边AB于点E，且与BC相切于点D，则该圆的圆心是（ ）
A、AE的垂直平分线与AC的垂直平分线的交点 B、AB的垂直平分线与AC的垂直平分线的交点 C、AE的垂直平分线与BC的垂直平分线的交点 D、AB的垂直平分线与BC的垂直平分线的交点7. 如图，⊙ 的直径 ， 是圆上任一点（A、B除外）， 的平分线交⊙ 于C，弦 过 ， 的中点 、 ，则 的长是（ ）
A、 B、 C、 D、8. 如图， 是半圆 的直径， 为弦， 于 ，过点 作 交半圆 于点 ，过点 作 于 ，若 ，则 的长为（ ）
A、 B、 C、 D、9.如图，圆O过点B、C，圆心O在正△ABC的内部，AB=2 ， OC=1，则圆O的半径为（ ）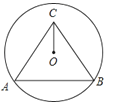
A、 B、2 C、 D、二、填空题
-
10. 如图，MN所在的直线垂直平分弦AB，利用这样的工具最少使用次，就可以找到圆形工件的圆心．
11. 如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，若∠C=15°，AB=6 cm，则⊙O半径为cm．
12. 如图，AB是⊙O的直径，点D平分弧AC，AC=5，DE=1.5，则OE= ．
三、解答题
-
13. 用工件槽（如图1）可以检测一种铁球的大小是否符合要求，已知工件槽的两个底角均为90°，尺寸如图（单位：cm）．将形状规则的铁球放入槽内时，若同时具有图1所示的A、B、E三个接触点，该球的大小就符合要求．图2是过球心O及A、B、E三点的截面示意图，求这种铁球的直径．
