2018-2019学年数学人教版九年级上册23.1 图形的旋转（2） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 如图，在△OAB中，∠AOB=55°，将△OAB在平面内绕点O顺时针旋转到△OA′B′ 的位置，使得BB′∥AO，则旋转角的度数为（ ）
A、125° B、70° C、55° D、15°2. 如图， 绕点O逆时针旋转80°得到 ，若∠AOB=35°，则∠AOD等于（ ）
A、35° B、40° C、45° D、55°3. 如图可以看作是一个等腰直角三角形旋转若干次而生成的，则每次旋转的度数可以是（ ）
A、90° B、60° C、45° D、30°4. 如图，将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC，连接AD，若∠B＝65°，则∠ADE等于（ ）
A、30° B、25° C、20° D、15°5. 如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6，将△ABC绕点C按逆时针方向旋转得到△A'B'C'，此时点A'恰好在AB边上，则点B'与点B之间的距离为（ ）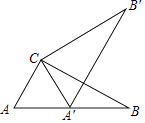
A、12 B、6 C、6 D、6. 如图，将 绕点A按逆时针方向旋转100°，得到 ，若点 在线段BC的延长线上，则 的大小为（ ）
A、70° B、80° C、84° D、86°7. 如图，将 绕点O逆时针旋转45°后得到 ，若 ，则 的度数是（ ）
A、25° B、30° C、35° D、40°8. 如图，将边长为 的正方形ABCD绕点A逆时针方向旋转30°后得到正方形 ，则图中阴影部分的面积为（ ）
A、 B、 C、 D、二、填空题
-
9. 如图，在等边三角形ABC中，AC＝9，点O在AC上，且AO＝3，点P是AB上的一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是 ．
10. 如图，在 中， ，以点C为中心，把 逆时针旋转45°，得到 ， 则图中阴影部分的面积为 ．
11. 如图，将 绕直角顶点C顺时针旋转90°，得到 ，连接AD，若 ，则 = ．
12. 如图，在 中 ，点D为BC中点，将 绕点D逆时针旋转45°，得到 ， 与AB交于点E，则 = ．
13. 如图，线段AB两端点坐标分别为 ，线段CD两端点坐标分别为 、D 数学课外兴趣小组研究这两线段发现：其中一条线段绕着某点旋转一个角度可得到另一条线段，请写出旋转中心的坐标 ．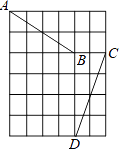
14. 如图，等边三角形ABC的边长为9cm， ，连接DE，将 绕点D逆时针旋转，得到 ，连接CF，则 =cm．
15. 如图，在 中， ，现将 绕点A逆时针旋转 得到 ，则阴影部分的面积为 ．
三、解答题
-
16. 如图所示，将△ABC绕其顶点A顺时针旋转30°后得△ADE．
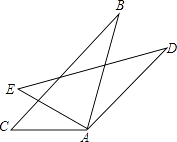(1)、问△ABC与△ADE的关系如何？
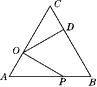
(2)、求∠BAD的度数．17. 如图，将Rt△ABC绕直角顶点C顺时针方向旋转38°得Rt△A′B′C，若AC⊥A′B′，求∠ABC的度数．
18. 如图，△ABC由△EDC绕C点旋转得到，B、C、E三点在同一条直线上，∠ACD=∠B，求证：△ABC是等腰三角形.
19. 如图，在正方形ABCD中，E为DC边上的点，连接BE，将 绕点C顺时针方向旋转 得到 ，连结EF，若 ，求 的度数．
20. 如图，点A′在Rt△ABC的边AB上，∠ABC=30°，AC=2，∠ACB=90°，△ACB绕顶点C按逆时针方向旋转与△A′CB′重合，A'B'与BC交于点D，连接BB′，求线段BB′的长度．
