2018-2019学年数学人教版八年级上册第12章 全等三角形 单元检测b卷
试卷更新日期：2018-10-10 类型：单元试卷
一、选择题
-
1. 如图，△ABC≌△EFD，且AB＝EF，EC＝4，CD＝3，则AC等于（ ）
A、3 B、4 C、7 D、82.要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在同一条直线上，如图，可以得到△EDC≌△ABC，所以ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC的理由是（ ）
A、SAS B、ASA C、SSS D、HL3. 如图，如果△ABC≌△DEF，∠B=25°，∠F=45°，那么∠A=（ ）
A、25° B、45° C、70° D、110°4. 如图，用直尺和圆规作一个角等于已知角，能得出 的依据是（ ）
A、（SAS） B、（SSS） C、（ASA） D、（AAS）5. 如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO 等于（ ）
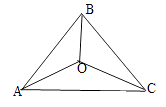A、1︰1︰1 B、1︰2︰3 C、2︰3︰4 D、3︰4︰56. 下列各条件中，不能作出唯一三角形的是（ ）A、已知两边和夹角 B、已知两角和夹边 C、已知两边和其中一边的对角 D、已知三边7. 如图，在△ABC中，∠B＝42°，AD⊥BC于点D，点E是BD上一点，EF⊥AB于点F，若ED＝EF，则∠AEC的度数为（ ）
A、60° B、62° C、64° D、66°8. 如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于点E，则下列结论：①AD平分∠CDE；②∠BAC＝∠BDE；③DE平分∠ADB；④BE＋AC＝AB．其中正确的有（ ）
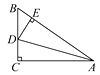A、1个 B、2个 C、3个 D、4个9. 如图，在△ABC和△CDE中，若∠ACB＝∠CED＝90°，AB＝CD，BC＝DE，则下列结论中不正确的是（ ）
A、△ABC≌△CDE B、CE＝AC C、AB⊥CD D、E为BC的中点10. 如图，已知AB∥CD，AD∥CB，则△ABC≌△CDA的依据是（ ）
A、SAS B、ASA C、AAS D、SSS11. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE.下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE.其中正确的有（ ）
A、4个 B、3个 C、2个 D、1个12. 如图，在 中， ，M，N，K分别是PA，PB，AB上的点，且 ， ，若 ，则 的度数为（ ）
A、 B、 C、 D、二、填空题
-
13. 如图，△ABC≌△ADE，若∠B=80°，∠C=30°，则∠EAD的度数为 ．
14. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F，若EF＝5 cm，则AE＝cm.
15. 如图，AB＝AC，BD⊥AC于D，CE⊥AB于E，CE，BD相交于点O，则图中全等的直角三角形有对．
16. 如图，已知相交直线AB和CD及另一直线MN，如果要在MN上找出与AB，CD距离相等的点，则这样的点至少有个，最多有个．
17. 如图，已知△ABC的三个内角的平分线交于点O，点D在CA的延长线上，且DC＝BC，若∠BAC＝80°，则∠BOD的度数为 ．
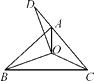
18. 如图， 中，P、Q分别是BC、AC上的点，作 ， ，垂足分别是R、S，若 ， ，下面四个结论：① ；② ；③ ≌ ；④AP垂直平分 其中正确结论的序号是 请将所有正确结论的序号都填上 ．
三、解答题
-
19. 如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F在AC上，BE＝FC，求证：BD＝DF.
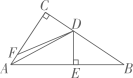
20. 如图，工人师傅要检查人字梁的∠B和∠C是否相等，但他手边没有量角器，只有一个刻度尺．他是这样操作的：①分别在BA和CA上取BE＝CG；②在BC上取BD＝CF；③量出DE的长为a m，FG的长为b m．如果a＝b，则说明∠B和∠C是相等的，他的这种做法合理吗？为什么？
21. 如图， ， ， 于D， 于E，且 ．求证： ．
22. 如图所示，已知△ABC中，D为BC上一点，E为△ABC外部一点，DE交AC于一点O，AC=AE，AD=AB，∠BAC=∠DAE．
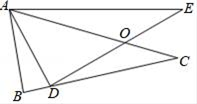(1)、求证：△ABC≌△ADE；
(2)、若∠BAD=20°，求∠CDE的度数．23. 已知：如图，在△ABC中，∠B=60°，D、E分别为AB、BC上的点，且AE、CD交于点F．若AE、CD为△ABC的角平分线．
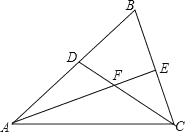(1)、求证：∠AFC=120°；(2)、若AD=6，CE=4，求AC的长？
24. 如图①，点A，E，F，C在同一直线上，AE＝CF，过点E，F分别作ED⊥AC，FB⊥AC，AB＝CD．
(1)、若BD与EF交于点G，试证明BD平分EF；
(2)、若将△DEC沿AC方向移动到图②的位置，其他条件不变，上述结论是否仍然成立？请说明理由．25. 如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°.
(1)、当点D在AC上时，如图①，线段BD，CE有怎样的数量关系和位置关系？请证明你的猜想；(2)、将图①中的△ADE绕点A顺时针旋转α(0°＜α＜90°)，如图②，线段BD，CE有怎样的数量关系和位置关系？请说明理由．26. 观察、猜想、探究：在 中， ．
(1)、如图 ，当 ，AD为 的角平分线时，求证： ；(2)、如图 ，当 ，AD为 的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想；(3)、如图 ，当AD为 的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．