2018-2019学年数学人教版八年级上册12.3 角的平分线的性质 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 如图，PC⊥OA于点C，PD⊥OB于点D，若PC＝PD，则（ ）
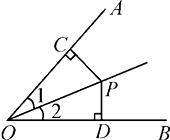A、∠1>∠2 B、∠1＝∠2 C、∠1<∠2 D、不能确定2. 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S△ABD=15，则CD的长为（ ）
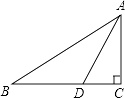A、3 B、4 C、5 D、63. 已知：如图，在△ABC中，∠C=90°，AD是角平分线，DE⊥AB，AB=5，AC=3，且S△ADC=6，则S△ABD=（ ）
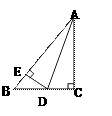A、4 B、10 C、8 D、不能确定4. 如图，已知DB⊥AE于B，DC⊥AF于C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=（ ）
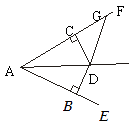A、130° B、150° C、100° D、140°5. 如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D，若CD=3，点Q是线段AB上的一个动点，则DQ的最小值（ ）
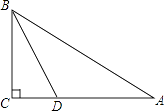A、5 B、4 C、3 D、26. 如图，DC⊥AC于C，DE⊥AB于E，并且DE＝DC，则下列结论中正确的是（ ）
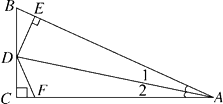A、DE＝DF B、BD＝FD C、∠1＝∠2 D、AB＝AC7. 如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，且∠ADC=110°，则∠MAB=（ ）
A、30° B、35° C、45° D、60°8. 如图，∠AOB=60°，以点O为圆心，以任意长为半径作弧交OA，OB于C，D两点；分别以C，D为圆心，以大于 CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上截取线段OM=6，则M点到OB的距离为（ ）
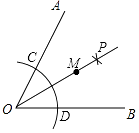A、6 B、2 C、3 D、二、填空题
-
9. 角平分线性质定理的逆定理：角的内部，到的点，在这个角的平分线上．
10. 如图，已知点P是 角平分线上的一点， ， ，M是OP的中点， ，如果点C是OB上一个动点，则PC的最小值为cm．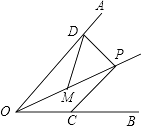
11. 如图，在Rt△ABC中，∠B=90°，以顶点C为圆心，适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于
EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D．若BD=3，AC=10，则△ACD的面积是 ．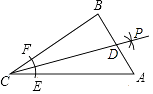 
12. 在△ABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于点D，DE⊥AB于点E，且AB=10，则△EDB的周长是；
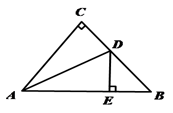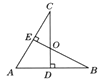
13. 随着人们生活水平的不断提高，汽车逐步进入到千家万户，小红的爸爸想在本镇的三条相互交叉的公路(如图所示)，建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有处.
14. 如图，在△ABC中，AB＝AC，∠BAC＝54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF(E在BC上，F在AC上)折叠，点C与点O恰好重合，则∠OEC＝ ．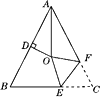
15. 如图， 于E， 于F，若 ， ，则下列结论： ； 平分 ； ； 中正确的是 ．
③④三、解答题
-
16. 如图所示，已知 △ABC的角平分线BM，CN相交于点P，求证点P到AB，BC，CA的距离相等．
17. 已知：OC平分∠AOB，点P、Q都是OC上不同的点，PE⊥OA，PF⊥OB，垂足分别为E、F，连接EQ、FQ.求证：FQ＝EQ
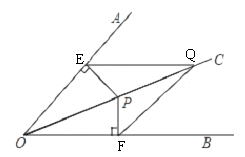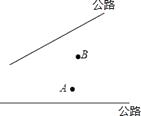
18. 如图所示，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB，交BC于D，能否在AB上确定一点E，使△BDE的周长等于AB的长?请说明理由．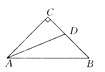
19. “西气东输”是造福子孙后代的创世纪工程。现有两条高速公路和A． B两个城镇(如图)，准备建立一个燃气中心站P，使中心站到两条公路距离相等，并且到两个城镇距离相等，请你画出中心站位置。
