2018-2019学年数学人教版八年级上册12.2 三角形全等的判定（3） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1. 下列条件中，不能判定△ABC≌△A′B′C′，的是（ ）A、∠A=∠A，∠C=∠C，AC=A′C′ B、∠B=∠B′，BC=B′C′，AB=A′B′ C、∠A=∠A′=80°，∠B=60°，∠C′=40°，AB=A′B′ D、∠A=∠A′，BC=B′C′，AB=A′B′2. 如图，已知AB=AD，使用“ ”能直接判定 的是（ ）
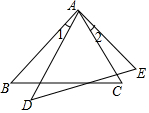
A、 B、 C、 D、3. 下列条件中，不能判定两个直角三角形全等的是（ ）A、两个锐角对应相等 B、一条直角边和一个锐角对应相等 C、两条直角边对应相等 D、一条直角边和斜边对应相等4. 如图1，D，E，F分别为△ABC边AC，AB，BC上的点，∠A=∠1=∠C，DE=DF.下面的结论一定成立的是（ ）
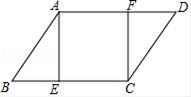
A、AE=FC B、AE=DE C、AE+FC=AC D、AD+FC=AB5. 如图所示，AB∥CD，AB=CD，BE=DF，则图中的全等三角形有（ ）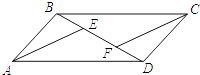
A、2对 B、3对 C、4对 D、5对6. 如图，若线段AB，CD互相平分且相交于点O，则下列结论错误的是（ ）
A、AD＝BC B、∠C＝∠D C、AD∥BC D、OB＝OC7. 如图，在△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长为（ ）
A、3 B、4 C、5 D、68. 下列条件中能判定△ABC≌△DEF的是（ ）A、AB＝DE，BC＝EF，∠A＝∠D B、∠A＝∠D，∠B＝∠E，∠C＝∠F C、AC＝DF，∠B＝∠F，AB＝DE D、∠B＝∠E，∠C＝∠F，AC＝DF二、填空题
-
9. 判定两个三角形全等除用定义外，还有几种方法，它们分别可以简写成；；；； ．10. 如图，AB=AC，点D，E分别在AB，AC上，CD，BE交于点F，只添加一个条件使△ABE≌△ACD，添加的条件是： ．
11. 如图，AB与CD相交于点O，且∠A＝∠B，AC＝BD，那么△ACO≌ ， 理由是 ．
12. 如图，已知点C是∠AOB平分线上一点，点E，F分别在边OA，OB上，如果要得到OE=OF，需要添加以下条件中的某一个即可，请你写出所有可能结果的序号为①∠OCE=∠OCF；②∠OEC=∠OFC；③EC=FC；④EF⊥OC．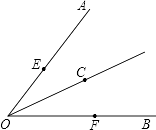
13. 如图，∠B=∠E=90°，AB=a，DE=b，AC=CD，∠D=60°，∠A=30°，则BE=.
14. 如图，∠ABF=∠DCE，BE=CF，请补充一个条件： ， 能使用“AAS”的方法得△ABF≌△DCE.
三、解答题
-
15. 已知：如下图，点A，F，E，C在同一直线上，AB∥CD，AB=CD，∠B=∠D．求证：⊿ABE≌⊿CDF。
