2018-2019学年数学人教版八年级上册12.2 三角形全等的判定（2） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
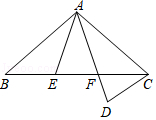
1. 如图，AD平分∠BAC，AB=AC，那么判定△ABD≌△ACD的理由是（ ）
A、SSS B、SAS C、ASA D、AAS2. 如图，AB∥DE，AF=DC，若要证明△ABC≌△DEF，还需补充的条件是（ ）
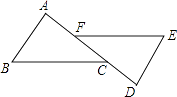A、AC=DF B、AB=DE C、∠A=∠D D、BC=EF3. 如图， ， ，判定 ≌ 的依据是（ ）
A、SSS B、SAS C、ASA D、HL4. 如图，AC与BD相交于点P，AP=DP，则需要“SAS”证明△APB≌△DPC，还需添加的条件是（ ）
A、BA=CD B、PB=PC C、∠A=∠D D、∠APB=∠DPC5.如图，已知△ABE≌△ACD，下列选项中不能被证明的等式是（ ）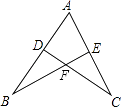
A、AD=AE B、DB=AE C、DF=EF D、DB=EC6. 如图，已知AB＝AC，AD＝AE，∠BAC＝∠DAE.下列结论不正确的是（ ）
A、∠BAD＝∠CAE B、△ABD≌△ACE C、AB＝BC D、BD＝CE7. 如图：等边三角形ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是（ ）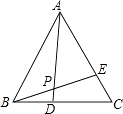
A、45° B、55° C、60° D、75°8. 在△ABC和△A′B′C′中，∠C＝∠C′，且b－a＝b′－a′，b＋a＝b′＋a′，则这两个三角形（ ）A、不一定全等 B、不全等 C、全等，根据“ASA” D、全等，根据“SAS”二、填空题
-
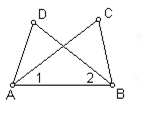
9. 如图，已知AC=BD，∠1=∠2，那么△ABC≌ ，其判定根据是。
10. 如图，在△ABC中，AB＝AC，AD平分∠BAC，则≌ ， 理由是 ．
11. 如图，OA＝OB，OC＝OD，∠D＝35°，则∠C等于；
12. 如图，若AB＝AD，∠BAC＝∠DAC，则△ABC≌△ADC，全等的依据是；
13. 如图所示，AC＝DF，BD＝EC，AC∥DF，∠ACB＝80°，∠B＝30°，则∠F＝.
14. 如图，△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC＝BC．若∠D＝20°，则∠ABC的度数为
15. 如图，AB与CD交于点O，OA＝OC，OD＝OB，∠A=50°，∠B＝30°，则∠D的度数为.
三、解答题
-
16. 如果AE∥CF，AE=CF，BE = DF．
求证：△AED≌△CFB．
17. 如图，已知△ABC和△DAE，D是AC上一点，AD=AB，DE∥AB，DE=AC．AE与BC相等吗？为什么？
18. 如图，已知AO＝DO，∠OBC＝∠OCB.求证：∠1＝∠2.
