2018-2019学年数学人教版八年级上册12.2 三角形全等的判定(1) 同步练习
试卷更新日期:2018-10-10 类型:同步测试
一、选择题
-
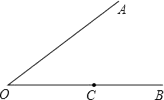
1. 如图,用尺规作一个角等于已知角,其作图原理是:由△ODC≌△O’D’C’得∠AOB=∠A’O’B’,其依据的定理是( )
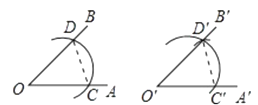 A、SSS B、SAS C、ASA D、AAS2. 如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( )
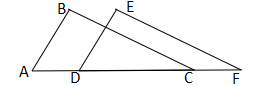
A、SSS B、SAS C、ASA D、AAS2. 如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE.可利用的是( ) A、①或② B、②或③ C、③或① D、①或④3. 如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( )
A、①或② B、②或③ C、③或① D、①或④3. 如图,在△ACE和△BDF中,AE=BF,CE=DF,要利用“SSS”证△ACE≌△BDF时,需添加一个条件是( ) A、AB=BC B、DC=BC C、AB=CD D、以上都不对4. 如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( )
A、AB=BC B、DC=BC C、AB=CD D、以上都不对4. 如图所示,已知AB=CD,AD=CB,AC、BD相交于O,则图中全等三角形有( ) A、2对 B、3对 C、4对 D、5对5. 如图, 中, , ,直接使用“SSS”可判定( )
A、2对 B、3对 C、4对 D、5对5. 如图, 中, , ,直接使用“SSS”可判定( )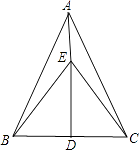 A、 ≌ B、 ≌ C、 ≌ D、 ≌6. 如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A、 ≌ B、 ≌ C、 ≌ D、 ≌6. 如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( ) A、1对 B、2对 C、3对 D、4对7. 若在△ABC和△A′B′C′中, ,则不正确的结论是( )
A、1对 B、2对 C、3对 D、4对7. 若在△ABC和△A′B′C′中, ,则不正确的结论是( )
A、△ABC≌△A′B′C′ B、三边对应相等 C、三对角对应相等 D、△ABC与△A′B′C′不全等8. 如图,AB=DE,AC=DF,BC=EF,则∠D等于( ) A、30° B、50° C、60° D、100°
A、30° B、50° C、60° D、100°二、填空题
-
9. 如图,AC=AD,BC=BD,则△ABC≌△;应用的判定方法是(简写) .
 10. 如图,若AB=DE, , BE=CF,则根据“SSS”可得△ABC≌△DEF.
10. 如图,若AB=DE, , BE=CF,则根据“SSS”可得△ABC≌△DEF. 11. 如图,AB=AC,BD=CD,若∠B=28°则∠C= 度;
11. 如图,AB=AC,BD=CD,若∠B=28°则∠C= 度;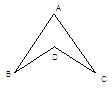 12. 如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是
12. 如图,小敏做了一个角平分仪ABCD,其中 , ,将仪器上的点A与 的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是 的平分线 此角平分仪的画图原理是:根据仪器结构,可得 ≌ ,这样就有 则说明这两个三角形全等的依据是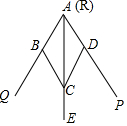 13. 如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是 .
13. 如图,AC、BD相交于点O,AB=DC﹑AO=DO,请你补充一个条件,使得△AOB≌△DOC(SSS).你补充的条件是 . 14. 请完善下面说明三角形全等的推理过程:
14. 请完善下面说明三角形全等的推理过程:如图,在△ABC和中,

∵ AB=AD (已知)
=DC (已知)
AC=
∴ △ABC ≌ (SSS)
15. 如图,AB=DE,AF=DC,EF=BC,∠AFB=70°,∠CDE=80°,∠ABC=.
三、解答题
-
16. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.试说明:∠A=∠D.
 17. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角.
17. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,求证:筝形ABCD的一条对角线BD平分一组对角. 18. 已知:如图,AD、BC相交于点O, , .
18. 已知:如图,AD、BC相交于点O, , .求证: .
 19. 如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.
19. 如图,点C、F、E、B在一条直线上,CD=BA,CE=BF,DF=AE,求证:∠B=∠C.