2018-2019学年数学北师大版九年级上册3.1 用树状图或表格求概率（3） 同步练习
试卷更新日期：2018-10-10 类型：同步测试
一、选择题
-
1.
如图的两个圆盘中均有5个数字，同时旋转两个圆盘，指针落在某一个数上的机会均等，那么两个指针同时落在奇数上的概率是（ ）
A、 B、 C、 D、2. 下面三张卡片上分别写有一个整式，把它们背面朝上洗匀，小明从中随机抽取一张卡片，再从剩下的卡片中随机抽取一张．第一次抽取的卡片上的整式做分子，第二次抽取的卡片上的整式做分母，则能组成分式的概率是（ ）
A、 B、 C、 D、3. 一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是（ ）
A、 B、 C、 D、4. 如图，已知点A，B，C，D是边长为1的正方形的顶点，连接任意两点均可得到一条线段，以下的树状图是所有可能发生的结果，在连接两点所得的所有线段中任取一条线段，取到长度为1的线段的概率为（ ）
A、 B、 C、 D、5. 某奥体中心的构造如图所示，其东、西面各有一个入口A，B，南面为出口C，北面分别有两个出口D，E.聪聪若任选一个入口进入，再任选一个出口离开，那么他从入口A进入并从北面出口离开的概率为（ ）
A、 B、 C、 D、6. 在如图的甲、乙两个转盘中，指针指向每一个数字的机会是均等的.当同时转动两个转盘，停止后指针所指的两个数字表示两条线段的长，如果第三条线段的长为5，那么这三条线段不能构成三角形的概率是（ ）
A、 B、 C、 D、7. 如图，甲为四等分数字转盘，乙为三等分数字转盘，同时自由转动两个转盘，当转盘停止转动后(若指针指在边界处则重转)，两个转盘指针指向数字之和不超过4的概率是（ ）
A、 B、 C、 D、8. 现有4张卡片，其中3张卡片正面上的图案是“
”，1张卡片正面上的图案是“ 
”，它们除此之外完全相同．把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案相同的概率是（ ）
A、 B、 C、 D、9. 如图，两个标有数字的轮子可以分别绕中心旋转，旋转停止时，每个轮子上的箭头各指向轮子上的一个数字，若左图上方箭头指着的数字为a，右图中指着的数字为b.数对(a，b)所有可能的个数为n，其中a+b恰为偶数的不同数对个数为m，则 等于（ ）
A、 B、 C、 D、10. 若一个袋子中装有形状与大小均完全相同的4张卡片，4张卡片上分别标有数字﹣2，﹣1，2，3，现从中任意抽出其中两张卡片分别记为x，y，并以此确定点P（x，y），那么点P落在直线y=﹣x+1上的概率是（ ）A、 B、 C、 D、二、填空题
-
11. 如图为一个电路图，在该电路图上有四个开关S1 ， S2 ， S3 ， S4和一个灯泡⊗，闭合开关S1或同时闭合开关S2 ， S3 ， S4都能够使灯泡发光，现在任意闭合其中两个开关，灯泡能够发光的概率为 ．
12. 如图，一个转盘被分成7个相同的扇形，颜色分为红、黄、绿三种，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，当作指向右边的扇形），则指针指向红色的概率为 ．
13. 如图，A，B是固定箭头的两个转盘.均被分成三个面积相等的扇形，转盘A上的扇形分别写有数字1，6，8，转盘B上的扇形分别写有数字4，5，7.如果你和小亮各选择其中一个转盘，同时将它们转动，规定如果转盘停止时，箭头指的数字较大者获胜.你认为选择转盘（填A或B）.
14. 如图所示，有三个形状与大小完全相同的直角三角形甲、乙、丙，其中任意两个平移后可拼成平行四边形或等腰三角形，则从中任意取出两个，能拼成等腰三角形的概率为 ．
15. 用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色．那么可配成紫色的概率是 ．
16. 从下面的6张牌中，一次任意抽取两张，则其点数和是奇数的概率为 ．
三、解答题
-
17.(1)、如图，将A、B、C三个字母随机填写在三个空格中（每空填一个字母，每空中的字母不重复），请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率；
(2)、若在如图三个空格的右侧增加一个空格，将A、B、C、D四个字母任意填写其中（每空填一个字母，每空中的字母不重复），从左往右字母顺序恰好是A、B、C、D的概率为 .18. 如图，羊年春节到了，小明亲手制作了3张一样的卡片，在每张卡片上分别写上“新”“年”“好”三个字，并随机放入一个不透明的信封中，然后让小芳分三次从信封中摸3张卡片（每次摸1张，摸出不放回）．
(1)、小芳第一次抽取的卡片是“新”字的概率是多少？
(2)、请通过画树状图或列表，求小芳先后抽取的3张卡片分别是“新年好”的概率．19. 数学课上，李老师准备了四张背面看上去无差别的卡片A，B，C，D，每张卡片的正面标有字母a，b，c表示三条线段（如图），把四张卡片背面朝上放在桌面上，李老师从这四张卡片中随机抽取一张卡片后不放回，再随机抽取一张．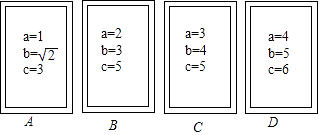
(1)、用树状图或者列表表示所有可能出现的结果；
(2)、求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率．
20. 将图中的三张扑克背面朝上放到桌面上，从中随机摸出两张，并用这两张扑克上的数字组成一个两位数，请你用画树状图或列表的方法求：
(1)、组成的两位数是偶数的概率；
(2)、组成的两位数是6的倍数的概率．
21. 转转盘和摸球是等可能概率下的经典模型．
(1)、如图，转盘的白色扇形和黑色扇形的圆心角分别为120°和240°．小莉让转盘自由转动2次，求指针2次都落在黑色区域的概率．(2)、小刚在一个不透明的口袋中，放入除颜色外其余都相同的18个小球，其中4个白球，6个红球，8个黄球．搅匀后，随机摸1个球，若事件A的概率与（1）中概率相同，请写出事件A．
22. 如图是一个平均被分成6等分的圆，每一个扇形中都标有相应的数字，甲乙两人分别转动转盘，设甲转动转盘后指针所指区域内的数字为x，乙转动转盘后指针所指区域内的数字为y（当指针在边界上时，重转一次，直到指向一个区域为止）．
(1)、直接写出甲转动转盘后所指区域内的数字为负数的概率；
(2)、用树状图或列表法，求出点（x，y）落在第二象限内的概率．
23. “五一”假日期间，某网店为了促销，设计了一种抽奖送积分活动，在该网店网页上显示如图所示的圆形转盘，转盘被均等的分成四份，四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样．参与抽奖的顾客只需用鼠标点击转盘，指针就会在转动的过程中随机的停在某个扇形区域，指针指向扇形上的积分就是顾客获得的奖励积分，凡是在活动期间下单的顾客，均可获得两次抽奖机会，求两次抽奖顾客获得的总积分不低于30分的概率．