2016-2017学年福建省福州教育学院二附中高三上学期期中物理试卷

试卷更新日期：2017-03-06 类型：期中考试

进入出卷网下载

一、选择题

1.
质量m=50kg的某同学站在观光电梯地板上，用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况（以竖直向上为正方向）．由图像提供的信息可知（）

A、在0～15s内，观光电梯上升的高度为25m B、在5～15s内，电梯内的同学处于超重状态 C、在20～25s与25～35s内，观光电梯的平均速度大小均为10m/s D、在25～35s内，观光电梯在减速上升，该同学的加速度大小2m/s²

查看试题解析
2. 为了节省能量，某商场安装了智能化的电动扶梯．无人乘行时，扶梯运转得很慢；有人站上扶梯时，它会先慢慢加速，再匀速运转．一顾客乘扶梯上楼，恰好经历了这两个过程，如图所示．那么下列说法中正确的是（）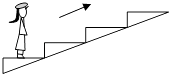

A、顾客始终受到三个力的作用 B、顾客始终处于超重状态 C、顾客对扶梯作用力的方向先指向左下方，再竖直向下 D、顾客对扶梯作用力的方向先指向右下方，再竖直向下

查看试题解析
3.
如图所示，某人坐在列车车厢内，观察悬挂在车厢顶上的摆球来判断列车的运动情况，得出下面一些结论，其中正确的是（）

A、摆球向前偏离竖直位置时，列车加速前进 B、摆球向后偏离竖直位置时，列车加速前进 C、摆球向后偏离竖直位置时，列车减速前进 D、摆球竖直下垂时，列车一定匀速前进

查看试题解析
4.
如图所示，物体沿斜面由静止滑下，在水平面上滑行一段距离后停止，物体与斜面和水平面间的动摩擦因数相同，斜面与水平面平滑连接．图中v、a、f和s分别表示物体速度大小、加速度大小、摩擦力大小和路程．图中正确的是（）

A、 B、 C、 D、

查看试题解析
5. 2014年12月14日，北京飞行控制中心传来好消息，嫦娥三号探测器平稳落月。已知嫦娥三号探测器在地球表面受的重力为G₁ ，绕月球表面飞行时受到月球的引力为G₂ ，地球的半径为R₁ ，月球的半径为R₂ ，地球表面处的重力加速为g。则（）

A、探测器沿月球表面轨道上做匀速圆周运动的周期为 $2 π \sqrt{\frac{R_{2} G_{1}}{g G_{2}}}$ B、月球与地球的质量之比为 $\frac{G_{1} R_{2}^{2}}{G_{2} R_{1}^{2}}$ C、月球表面处的重力加速度为 $\frac{G_{1}}{G_{2}} g$ D、月球与地球的第一宇宙速度之比为 $\sqrt{\frac{G_{1} R_{2}}{G_{2} R_{1}}}$

查看试题解析
6.
如图所示，在投球游戏中，某人将小球从P点以速度v水平抛向固定在水平地面上的塑料筐，小球恰好沿着筐的上沿入筐并打在筐的底角，若要让小球进入筐中并直接击中筐底正中间，下列说法不可行的是（）

A、在P点将小球以小于v的速度水平抛出 B、在P点将小球以大于v的速度水平抛出 C、在P点正上方某位置将小球以小于v的速度水平抛出 D、在P点正下方某位置将小球以小于v的速度水平抛出

查看试题解析
7.
如图，物块a、b和c的质量相同，a和b、b和c之间用完全相同的轻弹簧S₁和S₂相连，通过系在a上的细线悬挂于固定点O．整个系统处于静止状态．现将细线剪断．将物块a的加速度的大小记为a₁ ， S₁和S₂相对于原长的伸长分别记为△l₁和△l₂ ，重力加速度大小为g．在剪断的瞬间，（）

A、a₁=3g B、a₁=0 C、△l₁=2△l₂ D、△l₁=△l₂

查看试题解析
8.
如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为F，小球在最高点的速度大小为v，其F﹣v²象如乙图所示．则（）

A、小球的质量为 $\frac{a R}{b}$ B、当地的重力加速度大小为 $\frac{R}{b}$ C、v²=c时，杆对小球的弹力方向向上 D、v²=2b时，小球受到的弹力与重力大小相等

查看试题解析

二、计算题

9. 正以υ=30m/s的速度运行中的列车，接到前方小站的请求：在该站停靠1分钟接一位危重病人上车，司机决定以加速度大小a₁=0.6m/s²的匀减速直线运动到小站，停车1分钟后做加速度大小a₂=1.0m/s²的匀加速直线运动，又恢复到原来的速度．求：

(1)、司机从停车开始减速到恢复原来速度共经历的时间t；

(2)、司机由于临时停车共耽误的时间△t．

查看试题解析
10.
如图所示为中国月球探测工程的标志，它以中国书法的笔触，勾勒出一轮明月和一双踏在其上的脚印，象征着月球探测的终极梦想．一位勤于思考的同学，为探月宇航员设计了如下实验：在距月球表面高h处以初速度v₀水平抛出一个物体，然后测量出该平抛物体的水平位移为x．通过查阅资料知道月球的半径为R，引力常量为G，若物体只受月球引力的作用，请你求出：

(1)、月球表面的重力加速度；

(2)、月球的质量．

查看试题解析
11.
如图所示，摩托车做腾跃特技表演，沿曲面冲上高0.8m顶部水平高台，接着以v=3m/s水平速度离开平台，落至地面时，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑．A，B为圆弧两端点，其连线水平．已知圆弧半径为R=1.0m，人和车的总质量为180kg，特技表演的全过程中，阻力忽略不计．（计算中取g=10m/s² ， sin53°=0.8，cos53°=0.6）．求：

(1)、从平台飞出到A点，人和车运动的水平距离s．

(2)、从平台飞出到达A点时速度及圆弧对应圆心角θ．

(3)、人和车运动到达圆弧轨道A点时对轨道的压力．

(4)、人和车运动到圆弧轨道最低点O速度v′= $\sqrt{33}$ m/s此时对轨道的压力．

查看试题解析
12.
如图1，用一根长为L=1m的细线，一端系一质量为m=1kg的小球（可视为质点），另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ=37°，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T．求（g=10m/s² ， sin37°= $\frac{3}{5}$ ，cos37°= $\frac{4}{5}$ ，计算结果可用根式表示）：

(1)、若要小球离开锥面，则小球的角速度ω₀至少为多大？

(2)、若细线与竖直方向的夹角为60°，则小球的角速度ω′为多大？

(3)、
细线的张力T与小球匀速转动的加速度ω有关，当ω的取值范围在0到ω′之间时，请通过计算求解T与ω²的关系，并在图2坐标纸上作出T﹣ω²的图像，标明关键点的坐标值．

查看试题解析