2018-2019学年数学湘教版八年级上册第二章 三角形 单元过关检测
试卷更新日期：2018-09-30 类型：单元试卷
一、选择题
-
1. 到三角形三条边的距离都相等的点是这个三角形的（ ）A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点2. 下列命题不正确的是（ ）A、等腰三角形的底角不能是钝角 B、等腰三角形不能是直角三角形 C、若一个三角形有三条对称轴，那么它一定是等边三角形 D、两个全等的且有一个锐角为30°的直角三角形可以拼成一个等边三角形3.
如图，等腰△ABC的周长为19，底边BC=5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ）
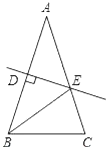A、9 B、10 C、11 D、124. 如图，BC⊥AC，BD⊥AD，且BC=BD，可说明三角形全等的方法是（ ）
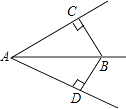A、SAS B、AAS C、SSA D、HL5. 如图，AB∥CD，∠D=30°，∠E=35°，则∠B的度数为（ ）
A、60° B、65° C、70° D、75°6. 如图，已知△ABC，AB=AC，若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（ ）
A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE7. 如图，给出下列四个条件，AB=DE，BC=EF，∠B=∠E，∠C=∠F，从中任选三个条件能使△ABC≌△DEF的共有（ ）
A、1组 B、2组 C、3组 D、4组8.如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB、下列确定P点的方法正确的是（ ）
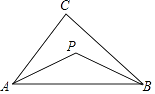A、P为∠A、∠B两角平分线的交点 B、P为AC、AB两边上的高的交点 C、P为AC、AB两边的垂直平分线的交点 D、P为∠A的角平分线与AB的垂直平分线的交点9. 如图所示，AB∥CD，EF⊥BD，垂足为E，∠1=50°，则∠2的度数为（ ）
A、50° B、40° C、45° D、25°10.如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是（ ）
A、10 B、15 C、20 D、3011. 如图，△ABC中，BO平分∠ABC，CO平分△ABC的外角∠ACD，MN经过点O，与AB，AC相交于点M，N，且MN∥BC，则BM，CN之间的关系是（ ）
A、BM+CN=MN B、BM﹣CN=MN C、CN﹣BM=MN D、BM﹣CN=2MN12.如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于D，则DE的长为（ ）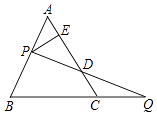
A、 B、 C、 D、二、填空题
-
13. 如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是 ．
14. 如图，已知AD⊥BC，若用HL判定△ABD≌△ACD，只需添加的一个条件是 ．
15. 如图，AC=BC，DC=EC，∠ACB=∠ECD=90°，且∠EBD=42°，则∠AEB= ．
16. 如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是 ．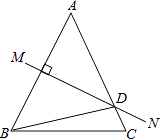
17. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为 ．
18. 如图，AB∥CD，以点B为圆心，小于DB长为半径作圆弧，分别交BA、BD于点E、F，再分别以点E、F，为圆心，大于 长为半径作圆弧，两弧交于点G，作射线BG交CD于点H。若∠D=116°，则∠DHB的大小为°。
三、解答题
-
19. 如图，已知：在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．
20. 如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点.试判断OE和AB的位置关系，并给出证明.
21. 如图，在△ABC中，∠B=90°，M是AC上任意一点（M与A不重合）MD⊥BC，交∠ABC的平分线于点D，求证：MD=MA．
22. 已知：如图，在△ABC中，
(1)、尺规作图：作△ABC的角平分线BD；(2)、在（1）的基础上，取BC的中点E，连接DE，若DE⊥BC，∠C=32°，求∠A的度数．23. 现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．
24. 如图，小明家有一个玻璃容器，他想测量一下它的内径是多少？但是他无法将刻度尺伸进去直接测量，于是他把两根长度相等的小木条AB，CD的中点连在一起，木条可以绕中点O自由转动，这样只要测量A，C的距离，就可以知道玻璃容器的内径，你知道其中的道理吗？请说明理由．
