2018-2019学年数学华师大版九年级上册第22章一元二次方程单元检测b卷

试卷更新日期：2018-09-30 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列方程是关于x的一元二次方程的是（）

A、x（x﹣1）=x² B、x²x=1 C、x²+x=1 D、（x²﹣1）²=1

查看试题解析
2. 把方程x（x+2）=3（x-1）化成一般式ax²+bx+c=0，则a、b、c的值分别是（）

A、1，-1，3 B、1，1，3 C、1，5，-3 D、1，-1，-3

查看试题解析
3. 用配方法解一元二次方程x²+4x﹣5=0，此方程可变形为（　　）

A、（x+2）²=9 B、（x﹣2）²=9 C、（x+2）²=1 D、（x﹣2）²=1

查看试题解析
4. 一元二次方程x²﹣3x﹣2=0的两根为x₁ ， x₂ ，则下列结论正确的是（）

A、x₁=﹣1，x₂=2 B、x₁=1，x₂=﹣2 C、x₁+x₂=3 D、x₁x₂=2

查看试题解析
5. 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成，其中甲、乙的面积和等于丙、丁的面积和．若丙的一股长为2，且丁的面积比丙的面积小，则丁的一股长为何？（）

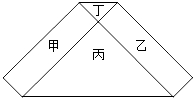A、 $\frac{1}{2}$ B、 $\frac{3}{5}$ C、2﹣ $\sqrt{3}$ D、4﹣2 $\sqrt{3}$

查看试题解析
6. 若关于x的一元二次方程x²﹣4x+5﹣a=0有实数根，则a的取值范围是（）

A、a≥1 B、a＞1 C、a≤1 D、a＜1

查看试题解析
7. 观察下列表格，一元二次方程x²﹣x=1.1的一个近似解是（）
x
1.4
1.5
1.6
1.7
1.8
1.9
x ²﹣x
0.56
0.75
0.96
1.19
1.44
1.71

A、0.11 B、1.19 C、1.73 D、1.67

查看试题解析
8. 设x，y为实数，5x²+4y²﹣8xy+2x+4的最小值为（）

A、1 B、2 C、3 D、5

查看试题解析
9. 有两个一元二次方程：M：ax²+bx+c=0；N：cx²+bx+a=0．其中a+c=0，以下列四个结论中，错误的是（）

A、如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 B、如果方程M有两根符号相同，那么方程N的两根符号也相同 C、如果5是方程M的一个根，那么 $\frac{1}{5}$ 是方程N的一个根 D、如果方程M和方程N有一个相同的根，那么这个根必是x=1

查看试题解析
10. 融侨半岛某文具店购入一批笔袋进行销售，进价为每个20元，当售价为每个50元时，每星期可以卖出100个，现需降价处理：售价每降价3元，每星期可以多卖出15个，店里每星期笔袋的利润要达到3125元．若设店主把每个笔袋售价降低x元，则可列方程为（）

A、（30+x）（100-15x）=3125 B、（30﹣x）(100+15x)=3125 C、（30+x）(100-5x)=3125 D、（30﹣x）(100+5x)=3125

查看试题解析

二、填空题

11. 关于x的方程（m﹣3） $x^{m^{2} - 7}$ ﹣x=5是一元二次方程，则m= ．

查看试题解析
12. 已知关于x的方程x²﹣2x+a=0有两个实数根，则实数a的取值范围是．

查看试题解析
13. 若实数a、b满足（4a+4b）（4a+4b﹣2）﹣8=0，则a+b= ．

查看试题解析
14. 方程2（1-x）²=3（x-1）的解是．

查看试题解析
15. 已知一元二次方程x²﹣3x﹣4=0的两根是m，n，则m²+n²= ．

查看试题解析
16. 对任意两实数a、b，定义运算“*”如下： $a * b = {\begin{matrix} b^{a} (a \geq b) \\ b^{a} + b (a < b) \end{matrix}$ . 根据这个规则，则方程 $2 * x$ ＝9的解为．

查看试题解析
17. 某一计算机的程序是：对于输入的每一个数，先计算这个数的平方的6倍，再减去这个数的4倍，再加上1，若一个数无论经过多少次这样的运算，其运算结果与输入的数相同，则称这个数是这种运算程序的不变数，这个运算程序的不变数是．

查看试题解析
18. 如图，长方形OABC的边OC、OA分别在x轴、y轴上，点B的坐标为（ $\sqrt{3}$ ，1）点D是AB边上一个动点（与点A不重合），沿OD将△OAD对折后，点A落到点P处，并满足△PCB是等腰三角形，则P点坐标为．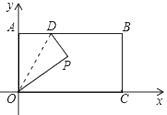

查看试题解析

三、解答题

19. 按指定的方法解下列方程：

(1)、2x²-5x-4=0（配方法）；

(2)、3（x-2）+x²-2x=0（因式分解法）；

(3)、（a²-b²）x²-4abx=a²-b²（a²≠b²）（公式法）．

查看试题解析
20. 已知关于x的方程x²﹣（2k﹣1）x+k²﹣3=0有两个实根x₁、x₂ ．

(1)、求k的取值范围；

(2)、若x₁、x₂满足x₁²+x₂²=5，求k的值．

查看试题解析
21. 关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(2)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
22. 关于x的一元二次方程（k﹣2）x²﹣2（k﹣1）x+k+1=0有两个不同的实数根是x_l和x₂ ．

(1)、求k的取值范围；

(2)、当k=﹣2时，求4x₁²+6x₂的值．

查看试题解析
23.

(1)、已知 $m + n = 8 ， m n = 15$ 求 $m^{2} - m n + n^{2}$ 的值

(2)、已知 $a^{2} + a - 1 = 0$ 求 $a^{3} + 2 a^{2} + 2016$ 的值

(3)、已知 $a + \frac{1}{a} = \sqrt{7}$ ，求 $a - \frac{1}{a}$ 的值

查看试题解析
24. 近期猪肉价格不断走高，引起了民众与政府的高度关注．当市场猪肉的平均价格每千克达到一定的单价时，政府将投入储备猪肉以平抑猪肉价格．

(1)、从今年年初至5月20日，猪肉价格不断走高，5月20日比年初价格上涨了60%．某市民在今年5月20日购买2.5千克猪肉至少要花100元钱，那么今年年初猪肉的最低价格为每千克多少元？

(2)、5月20日，猪肉价格为每千克40元.5月21日，某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售．某超市按规定价出售一批储备猪肉，该超市在非储备猪肉的价格仍为每千克40元的情况下，该天的两种猪肉总销量比5月20日增加了a%，且储备猪肉的销量占总销量的 $\frac{3}{4}$ ，两种猪肉销售的总金额比5月20日提高了 $\frac{1}{10}$ a%，求a的值．

查看试题解析
25. 如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．

(1)、当t为何值时，P、Q两点的距离为5 $\sqrt{2}$ cm？

(2)、当t为何值时，△PCQ的面积为15cm²？

(3)、请用配方法说明，点P运动多少时间时，四边形BPQA的面积最小？最小面积是多少？

查看试题解析
26. 阅读下列材料，并用相关的思想方法解决问题．
计算：（1﹣ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ）×（ $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$ + $\frac{1}{5}$ ）﹣（1﹣ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ﹣ $\frac{1}{5}$ ）×（ $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$ ）．
令 $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$ =t，则
原式=（1﹣t）（t+ $\frac{1}{5}$ ）﹣（1﹣t﹣ $\frac{1}{5}$ ）t
=t+ $\frac{1}{5}$ ﹣t²﹣ $\frac{1}{5}$ t﹣ $\frac{4}{5}$ t+t²
= $\frac{1}{5}$
问题：

(1)、计算
（1﹣ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ﹣…﹣ $\frac{1}{2014}$ ）×（ $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$ + $\frac{1}{5}$ +…+ $\frac{1}{2014}$ + $\frac{1}{2015}$ ）﹣（1﹣ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ﹣ $\frac{1}{5}$ ﹣…﹣ $\frac{1}{2014}$ ﹣ $\frac{1}{2015}$ ）×（ $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{4}$ +…+ $\frac{1}{2014}$ ）；

(2)、解方程（x²+5x+1）（x²+5x+7）=7．

查看试题解析

x	1.4	1.5	1.6	1.7	1.8	1.9
x ²﹣x	0.56	0.75	0.96	1.19	1.44	1.71

2018-2019学年数学华师大版九年级上册第22章 一元二次方程单元检测b卷

一、选择题

二、填空题

三、解答题

2018-2019学年数学华师大版九年级上册第22章一元二次方程单元检测b卷