浙江省温州市2018届六校联考数学试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. ﹣5的绝对值是( )
A、5 B、1 C、0 D、﹣52. 右图是七(1)班40名同学在校午餐所需时间的频数直 方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )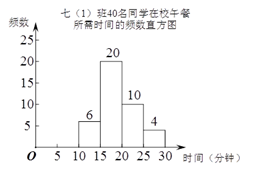 A、10~15分钟 B、15~20分钟 C、20~25分钟 D、25~30分钟3. 如图所示的几何体的主视图为( )
A、10~15分钟 B、15~20分钟 C、20~25分钟 D、25~30分钟3. 如图所示的几何体的主视图为( )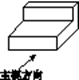 A、
A、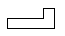 B、
B、 C、
C、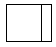 D、
D、 4. 一次函数y=2x+6图象与y轴的交点坐标是( )
4. 一次函数y=2x+6图象与y轴的交点坐标是( )
A、(-3,0) B、(3,0) C、(0,-6) D、(0,6)5. 在一个不透明的袋中,装有3个黄球,2个红球和5个白球,它们除颜色外其它都相同,从袋中任意摸出一个球,是红球的概率是( )
A、 B、 C、 D、6. 如图,在△ABC中,∠C=90°,AB=13,BC=5,则cosA的值是( )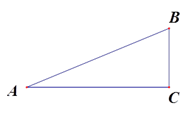 A、 B、 C、 D、7. 已知,方程组 的解为 ,现给出另一个方程组 ,它的解为( )
A、 B、 C、 D、7. 已知,方程组 的解为 ,现给出另一个方程组 ,它的解为( )
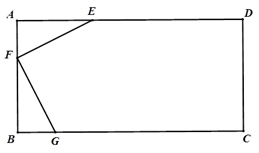
A、 B、 C、 D、8. 如图,矩形ABCD和菱形EFGH均以直线HF、EG为对称轴,边EH分别交AB,AD于点M,N,若M,N分别为EH的三等分点,且菱形EFGH的面积与矩形ABCD的面积之差为S,则菱形EFGH的面积等于( ) A、7S B、8S C、9S D、10S9. 如图,将正五边形绕其中心O顺时针旋转ɑ角度,与原正五边形构成新的图形,若要使该图形是中心对称图形,则ɑ的最小角度为( )
A、7S B、8S C、9S D、10S9. 如图,将正五边形绕其中心O顺时针旋转ɑ角度,与原正五边形构成新的图形,若要使该图形是中心对称图形,则ɑ的最小角度为( )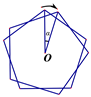 A、30° B、36° C、72° D、9010. 如图,把边长为a cm的等边△ABC剪成四部分,从三角形三个顶点往下b cm处,呈 30°角 下剪刀,使中间部分形成一个小的等边△DEF.若△DEF的面积是△ABC的 ,则 的值为( )
A、30° B、36° C、72° D、9010. 如图,把边长为a cm的等边△ABC剪成四部分,从三角形三个顶点往下b cm处,呈 30°角 下剪刀,使中间部分形成一个小的等边△DEF.若△DEF的面积是△ABC的 ,则 的值为( )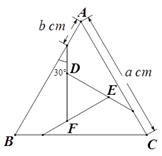 A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
11.
(1)、计算:(2)、化简: .12. 如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F. (1)、求证:△AEF≌△DEB;(2)、若∠BAC=90°,AF=6,求AD的长.13. 国学经典进校园,传统文化润心灵,某校开设了“围棋入门”、“诗歌汉字”、“翰墨飘香”、“史学经典”四门拓展课(每位学生必须且只选其中一门).
(1)、求证:△AEF≌△DEB;(2)、若∠BAC=90°,AF=6,求AD的长.13. 国学经典进校园,传统文化润心灵,某校开设了“围棋入门”、“诗歌汉字”、“翰墨飘香”、“史学经典”四门拓展课(每位学生必须且只选其中一门).
(1)、学校对八年级部分学生进行选课调查,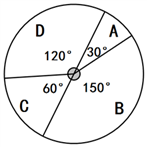

得到如图所示的统计图,请估计该校八年级420名学生选“诗歌汉字”的人数.
(2)、“翰墨飘香”书画社的甲、乙、丙三人的书法水平相当,学校决定从这三名同学中任选两名参加市书法比赛,求甲和乙被选中的概率.(要求列表或画树状图)
14. 如图,在方格纸中,点A,D都在格点上,作三角形ABC,使其满足下列条件.(点B,C不与点D重合)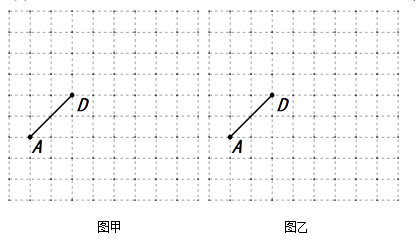 (1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.
(1)、在图甲中,作格点等腰△ABC,使AD为△ABC的高线.
(2)、在图乙中,作格点钝角△ABC,使AD为△ABC的角平分线
15. 已知:如图,△ABC内接于⊙O,AB为直径,点D是弧AC的中点,连结BD交AC于点E,过D点作⊙O的切线交BC的延长线于F.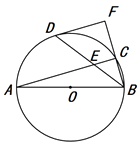 (1)、求证:∠FDB = ∠AED.(2)、若⊙O 的半径为5,tan∠FBD= ,求CF的长.
(1)、求证:∠FDB = ∠AED.(2)、若⊙O 的半径为5,tan∠FBD= ,求CF的长.
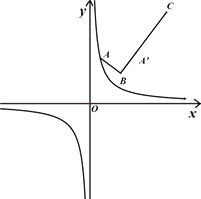
16. 某公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆来完成此项任务. 已知每辆甲种货车一次最多运送机器45台、租车费用400元,每辆乙种货车一次最多运送机器30台租车费用280元. 设租用甲种货车 辆( 为正整数)(1)、请用含 的代数式表示租车费用;(2)、存在能完成此项运送任务的最节省费用的租车方案吗?若存在,请计算并给出租车方案;若不存在,请说明理由.17. 如图,抛物线 交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分别交x轴、AC于点E、F,点P是射线DE上一动点,过点P作AC的平行线MN交x轴于点H,交抛物线于点M,N(点M位于对称轴的左侧).设点P的纵坐标为t..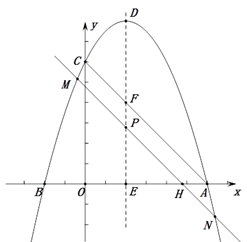 (1)、求抛物线的对称轴及点A的坐标.(2)、当点P位于EF的中点时,求点M的坐标.(3)、① 点P在线段DE上运动时,当 时,求t的值.18. 如图,等边三角形ABC中,AB= ,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延长线于点D,连结CD. 点E为线段AD上一点(不与点A,D重合),过点E作EF∥AB交BC于点F,以EF为直径作⊙O. 设AE的长为 .
(1)、求抛物线的对称轴及点A的坐标.(2)、当点P位于EF的中点时,求点M的坐标.(3)、① 点P在线段DE上运动时,当 时,求t的值.18. 如图,等边三角形ABC中,AB= ,AH⊥BC于点H,过点B作BD⊥AB交线段AH的延长线于点D,连结CD. 点E为线段AD上一点(不与点A,D重合),过点E作EF∥AB交BC于点F,以EF为直径作⊙O. 设AE的长为 .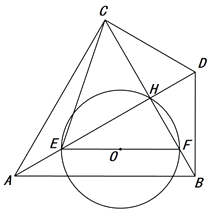 (1)、求线段CD的长度.
(1)、求线段CD的长度.
(2)、当点E在线段AH上时,用含x的代数式表示EF的长度.(3)、当⊙O与四边形ABDC的一边所在直线相切时,求所有满足条件的 的值.
三、填空题
-
19. 因式分解: .
20. 一次数学检测中,某小组六位同学的成绩分别是100,95,80,85,80,93则这六个数据的中位数是.
21. 若一个多边形的内角和是1800°,则这个多边形的边数是;
22. 有20人外出旅游,因特殊原因,服务员在安排房间时每个房间比原来多住了1人,结果比原来少用了一个房间,若原来每间住 人,则可列关于 的方程是.