浙江省杭州市拱墅区2018届数学中考二模试卷
试卷更新日期：2018-09-30 类型：中考模拟
一、单选题
-
1. （﹣2）2=（ ）A、 B、- C、4 D、﹣42. 2018年五一小长假，杭州市公园、景区共接待游客总量617.57万人次，用科学记数法表示617.57万的结果是（ ）A、 6.1757×105 B、6.1757×106 C、0.61757×106 D、0.61757×1073. 四张分别画有平行四边形、等腰直角三角形、正五边形、圆的卡片，它们的背面都相同，现将它们背面朝上，从中任取一张，卡片上所画图形恰好是中心对称图形的概率是（ ）
A、 B、 C、 D、4. 下表是某校乐团的年龄分布，其中一个数据被遮盖了，下面对于中位数的说法正确的是（ ）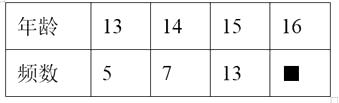
A、中位数是14 B、中位数可能是14.5 C、中位数是15或15.5 D、中位数可能是165. 当x=1时，代数式x3+x+m的值是7，则当x=﹣1时，这个代数式的值是（ ）
A、7 B、3 C、1 D、﹣76. 某班分两组志愿者去社区服务，第一组20人，第二组26人．现第一组发现人手不够，需第二组支援．问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍？设抽调x人，则可列方程（ ）
A、20=2（26﹣x） B、20+x=2×26 C、2（20+x）=26﹣x D、20+x=2（26﹣x）7. 如图，已知直线a∥b∥c，直线m分别交直线a、b、c于点A，B，C，直线n分别交直线a、b、c于点D，E，F，若 ， ，则 的值应该（ ）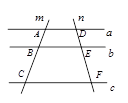
A、等于 B、大于 C、小于 D、不能确定8. 方程 =0的解的个数为（ ）
A、0个 B、1个 C、2个 D、3个9. 二次函数y=﹣x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x2+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）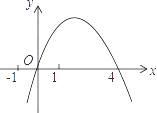
A、t＞﹣5 B、﹣5＜t＜3 C、3＜t≤4 D、﹣5＜t≤410. 如图，已知E、F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤AM= MF．其中正确结论的个数是（ ）
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 分解因式：a3-16a=。12. 已知2x（x+1）=x+1，则x= ．
13. 一个仅装有球的不透明布袋里共有4个球（只有颜色不同），其中3个是红球，1个是白球，从中任意摸出一个球，记下颜色后不放回，搅匀，再任意摸出一个球，则两次摸出都是红球的概率是 ．
14. 已知一块直角三角形钢板的两条直角边分别为30cm、40cm，能从这块钢板上截得的最大圆的半径为 ．
15. 如图，点A是双曲线y=﹣ 在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= 上运动，则k的值为 ．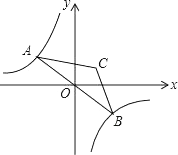
16. 如图，⊙O的半径为2，弦BC=2 ，点A是优弧BC上一动点（不包括端点），△ABC的高BD、CE相交于点F，连结ED．下列四个结论：①∠A始终为60°；②当∠ABC=45°时，AE=EF；③当△ABC为锐角三角形时，ED= ；④线段ED的垂直平分线必平分弦BC．其中正确的结论是 ． （把你认为正确结论的序号都填上）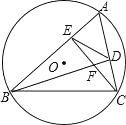
三、解答题
-
17. 某校实验课程改革，初三年级设罝了A，B，C，D四门不同的拓展性课程（每位学生只选修其中一门，所有学生都有一门选修课程），学校摸底调査了初三学生的选课意向，并将调查结果绘制成两个不完整的统计图，问该校初三年级共有多少学生？其中要选修B、C课程的各有多少学生？
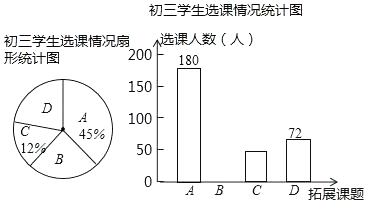18. 在平面直角坐标系中，二次函数y=x2+bx+c（b，c都是常数）的图象经过点（1，0）和（0，2）．(1)、当﹣2≤x≤2时，求y的取值范围．(2)、已知点P（m，n）在该函数的图象上，且m+n=1，求点P的坐标．19. 已知：如图，△ABC中，AB＝2，BC＝4，D为BC边上一点，BD＝1．
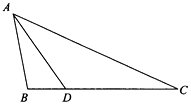(1)、求证：△ABD∽△CBA；(2)、在原图上做DE∥AB交AC于点E，请直接写出另一个与∆ABD相似的三角形，并求出DE的长。20. 某化工车间发生有害气体泄漏，自泄漏开始到完全控制利用了40min，之后将对泄漏有害气体进行清理，线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x（min）之间的函数关系（0≤x≤40），反比例函数y= 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x（min）之间的函数关系（40≤x≤？）．根据图象解答下列问题：
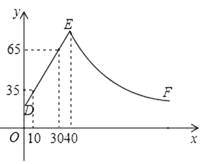(1)、危险检测表在气体泄漏之初显示的数据是；
(2)、求反比例函数y= 的表达式，并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值．
21. 如图，以⊿ABC的一边AB为直径的半圆与其它两边AC，BC的交点分别为D，E，且 ．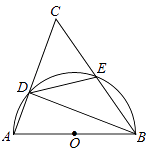
(1)、试判断⊿ABC的形状，并说明理由；
(2)、已知半圆的半径为5，BC=12，求 的值．22. 已知y关于x的二次函数y=ax2﹣bx+2（a≠0）．
(1)、当a=﹣2，b=﹣4时，求该函数图象的对称轴及顶点坐标．
(2)、在（1）的条件下，Q（m，t）为该函数图象上的一点，若Q关于原点的对称点P也落在该函数图象上，求m的值．(3)、当该函数图象经过点（1，0）时，若A（ ，y1），B（ ，y2）是该函数图象上的两点，试比较y1与y2的大小．
23. 已知边长为3的正方形ABCD中，点E在射线BC上，且BE=2CE，连接AE交射线DC于点F，若△ABE沿直线AE翻折，点B落在点B1处．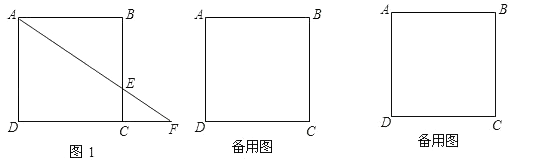
(1)、如图1，若点E在线段BC上，求CF的长；
(2)、求sin∠DAB1的值；(3)、如果题设中“BE=2CE”改为“ =x”，其它条件都不变，试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围（只要写出结论，不需写出解题过程）．