河南省驻马店市正阳县2018届数学中考二模试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、2018 D、﹣20182. 俗话说:“水滴石穿”,水滴不断的落在一块石头的同一个位置,经过若干年后,石头上形成了一个深度为0.000000039cm的小洞,则0.000000039用科学记数法可表示为( )A、3.9×10﹣8 B、﹣3.9×10﹣8 C、0.39×10﹣7 D、39×10﹣93. “2018年平昌冬季奥运会”的颁奖台如图所示,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、x2+x2=x4 B、a3•a2=a6 C、(2x2)3=6x6 D、|1﹣ |= ﹣15. 某人打靶五次的环数如下:1,4,6,8,x,其中整数x是这组数据的中位数,那么这组数据的平均数是( )A、4.8 B、4.8或5 C、4.6或4.8 D、4.6或4.8或56. 不等式组 的非正整数解的个数是( )A、4 B、5 C、6 D、77. 如图,在△ABC中,AB=AC,若以点B为圆心,BC长为半径作弧,交AC于点E,则下列结论一定正确的是( )
4. 下列运算正确的是( )A、x2+x2=x4 B、a3•a2=a6 C、(2x2)3=6x6 D、|1﹣ |= ﹣15. 某人打靶五次的环数如下:1,4,6,8,x,其中整数x是这组数据的中位数,那么这组数据的平均数是( )A、4.8 B、4.8或5 C、4.6或4.8 D、4.6或4.8或56. 不等式组 的非正整数解的个数是( )A、4 B、5 C、6 D、77. 如图,在△ABC中,AB=AC,若以点B为圆心,BC长为半径作弧,交AC于点E,则下列结论一定正确的是( )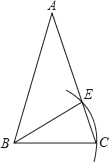 A、AE=BE B、BE是∠ABC的角平分线 C、∠A=∠EBC D、AE=BC8. 如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )
A、AE=BE B、BE是∠ABC的角平分线 C、∠A=∠EBC D、AE=BC8. 如图,在△ABC中,点D,E,F分别是边AB,AC,BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( ) A、AB=AC B、AB=BC C、BE平分∠ABC D、EF=CF9. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
A、AB=AC B、AB=BC C、BE平分∠ABC D、EF=CF9. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )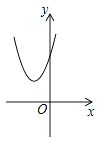 A、
A、 B、
B、 C、
C、 D、
D、 10.
10.如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
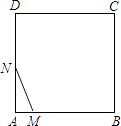 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. +(﹣2)0= .12. 若点M(x1 , y1)在函数y=kx+b(k≠0)的图象上,当﹣1≤x1≤2时,﹣2≤y1≤1,则这条直线的函数解析式为 .13. 若关于x的一元二次方程(1﹣k)x2+2kx﹣k+1=0有实数根,则实数k的取值范围是 .14. 如图,在Rt△ABC中,∠B=60°,AB=1,现将△ABC绕点A逆时针旋转至点B恰好落在BC上的B'处,其中点C运动路径为 ,则图中阴影部分的面积是 .
 15. 如图,等边三角形ABC的边长为2,D,E分别是边AB,AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为 .
15. 如图,等边三角形ABC的边长为2,D,E分别是边AB,AC上的点,沿DE所在的直线折叠∠A,使点A的对应点P始终落在边BC上,若△BDP是直角三角形,则AD的长为 .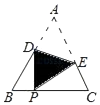
三、解答题
-
16. 先化简,再求值: ,其中x是方程x2﹣3x﹣4=0的一个解.17. 电视热播节目“最强大脑”激发了学生的思考兴趣,为满足学生的需求,某学校抽取部分学生举行“最强大脑”选拔赛,针对竞赛成绩分成以下六个等级A:0~50分;B:51~60分;C:61~70分;D:71~80分;E:81~90分;F:91~100分,根据调查结果绘制了如下尚不完整的统计图,请你根据统计图解答下列问题:
 (1)、此次竞赛抽取的总人数为 , 请补全条形统计图;(2)、若全市约有3万名在校学生,试估计全市学生中竞赛成绩在71~90分的人数约有多少?(3)、若在此次接受调查的学生中,随机抽查一人,则此人的成绩在80分以上的概率是多少?18. 如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC交AC于点E,延长ED交AB的延长线于点F.
(1)、此次竞赛抽取的总人数为 , 请补全条形统计图;(2)、若全市约有3万名在校学生,试估计全市学生中竞赛成绩在71~90分的人数约有多少?(3)、若在此次接受调查的学生中,随机抽查一人,则此人的成绩在80分以上的概率是多少?18. 如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC交AC于点E,延长ED交AB的延长线于点F. (1)、求证:DE是⊙O的切线;(2)、若AB=8,AE=6,求BF的长.19. 位于河南省郑州市的炎黄二帝巨型塑像,是为代表中华民族之创始、之和谐、之统一.塑像由山体CD和头像AD两部分组成.某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°,头像A处的仰角为70.5°,求头像AD的高度.(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
(1)、求证:DE是⊙O的切线;(2)、若AB=8,AE=6,求BF的长.19. 位于河南省郑州市的炎黄二帝巨型塑像,是为代表中华民族之创始、之和谐、之统一.塑像由山体CD和头像AD两部分组成.某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°,头像A处的仰角为70.5°,求头像AD的高度.(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)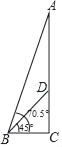 20. 如图,一次函数y=x﹣2与反比例函数y= (x>0)的图象相交于点M(m,1).
20. 如图,一次函数y=x﹣2与反比例函数y= (x>0)的图象相交于点M(m,1). (1)、填空:m的值为 , 反比例函数的解析式为;(2)、已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y= (x>0)的图象与点B,试用n表示△NAB的面积S.21. 植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.(1)、求一棵甲种树苗和一棵乙种树苗的售价各是多少元?(2)、学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.22. 如图:
(1)、填空:m的值为 , 反比例函数的解析式为;(2)、已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y= (x>0)的图象与点B,试用n表示△NAB的面积S.21. 植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.(1)、求一棵甲种树苗和一棵乙种树苗的售价各是多少元?(2)、学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.22. 如图: (1)、观察猜想:
(1)、观察猜想:在Rt△ABC中,∠BAC=90°,AB=AC,点D在边BC上,连接AD,把△ABD绕点A逆时针旋转90°,点D落在点E处,如图①所示,则线段CE和线段BD的数量关系是 , 位置关系是 .
(2)、探究证明:在(1)的条件下,若点D在线段BC的延长线上,请判断(1)中结论是还成立吗?请在图②中画出图形,并证明你的判断.
(3)、拓展延伸:如图③,∠BAC≠90°,若AB≠AC,∠ACB=45°,AC= ,其他条件不变,过点D作DF⊥AD交CE于点F,请直接写出线段CF长度的最大值.
23. 如图,在平面直角坐标系中,直线l:y=kx+h与x轴相交于点A(﹣1,0),与y轴相交于点C,与抛物线y=﹣x2+bx+3的一交点为点D,抛物线过x轴上的AB两点,且CD=4AC. (1)、求直线l和抛物线的解析式;(2)、点E是直线l上方抛物线上的一动点,求当△ADE面积最大时,点E的坐标;(3)、设P是抛物线对称轴上的一点,点Q在抛物线上,四边形APDQ能否为矩形?若能,请直接写出点P的坐标;若不能,请说明理由.
(1)、求直线l和抛物线的解析式;(2)、点E是直线l上方抛物线上的一动点,求当△ADE面积最大时,点E的坐标;(3)、设P是抛物线对称轴上的一点,点Q在抛物线上,四边形APDQ能否为矩形?若能,请直接写出点P的坐标;若不能,请说明理由.