河南省商丘市柘城县2018届数学中考模拟试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. ﹣2018的绝对值是( )A、±2018 B、﹣2018 C、﹣ D、20182. 据相关报道,开展精准扶贫工作五年以来,我国约有55000000人摆脱贫困,将55000000用科学记数法表示是( )A、55×106 B、0.55×108 C、5.5×106 D、5.5×1073.
如图所示的几何体的俯视图是( )
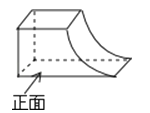 A、
A、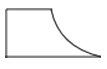 B、
B、 C、
C、 D、
D、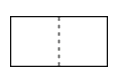 4. 下列各式计算正确的是( )A、(b+2a)(2a﹣b)=b2﹣4a2 B、2a3+a3=3a6 C、a3•a=a4 D、(﹣a2b)3=a6b35. 某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )
4. 下列各式计算正确的是( )A、(b+2a)(2a﹣b)=b2﹣4a2 B、2a3+a3=3a6 C、a3•a=a4 D、(﹣a2b)3=a6b35. 某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )成绩(分)
30
29
28
26
18
人数(人)
32
4
2
1
1
A、该班共有40名学生 B、该班学生这次考试成绩的平均数为29.4分 C、该班学生这次考试成绩的众数为30分 D、该班学生这次考试成绩的中位数为28分6. 已知关于x的一元二次方程x2+2x﹣(m﹣2)=0有实数根,则m的取值范围是( )A、m>1 B、m<1 C、m≥1 D、m≤17. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为( )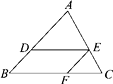 A、6 B、8 C、10 D、128. 如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( )
A、6 B、8 C、10 D、128. 如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为( ) A、4 B、﹣4 C、﹣6 D、69. 如图,直角三角形ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为( )
A、4 B、﹣4 C、﹣6 D、69. 如图,直角三角形ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为( ) A、2π﹣ B、π+ C、π+2 D、2π﹣210. 现有四张分别标有数字1、2、2、3的卡片,他们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽出一张后放回,再背朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率( )A、 B、 C、 D、
A、2π﹣ B、π+ C、π+2 D、2π﹣210. 现有四张分别标有数字1、2、2、3的卡片,他们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽出一张后放回,再背朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率( )A、 B、 C、 D、二、解答题
-
11. 先化简 ,然后从﹣ <x< 的范围内选取一个合适的整数作为x的值代入求值.12. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
 (1)、①表中a的值为 , 中位数在第组;②频数分布直方图补充完整 ;
(1)、①表中a的值为 , 中位数在第组;②频数分布直方图补充完整 ;
(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.13. 如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C. (1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为6,BC=8,求弦BD的长.14. 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为6,BC=8,求弦BD的长.14. 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 15. 如图,∠AOB=90°,反比例函数y=﹣ (x<0)的图象过点A(﹣1,a),反比例函数y= (k>0,x>0)的图象过点B,且AB∥x轴.
15. 如图,∠AOB=90°,反比例函数y=﹣ (x<0)的图象过点A(﹣1,a),反比例函数y= (k>0,x>0)的图象过点B,且AB∥x轴.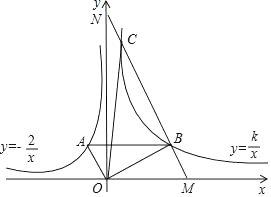 (1)、求a和k的值;(2)、过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y= 于另一点C,求△OBC的面积.16. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、求a和k的值;(2)、过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y= 于另一点C,求△OBC的面积.16. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)、实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.17. 如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE= AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.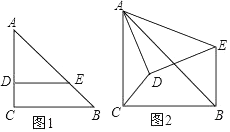 (1)、问题发现
(1)、问题发现①当θ=0°时, =;
②当θ=180°时, = .
(2)、拓展探究试判断:当0°≤θ<360°时, 的大小有无变化?请仅就图2的情形给出证明;
(3)、问题解决①在旋转过程中,BE的最大值为;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .
18. 如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B. (1)、求该抛物线的函数表达式;(2)、若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;(3)、如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
(1)、求该抛物线的函数表达式;(2)、若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;(3)、如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.三、填空题
-
19. = .20. 不等式组 的非负整数解的个数是 .


