河南省南阳市淅川县2018届数学中考一模试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最大的数是A、5 B、 C、0 D、2. 下列运算中,结果正确的是A、 B、 C、 D、3. 据新华社北京2017年1月20日电国家统计局20日发布数据,初步核算,2016年我国国内生产总值 约74万亿元,若将74万亿用科学记数法表示为A、 B、 C、 D、4. 方程 的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为A、6 B、8 C、10 D、8或105. 右图是由6个小正方体搭建而成的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )
6. 某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )成绩(分)
30
29
28
26
18
人数(人)
32
4
2
1
1
A、该班共有40名学生 B、该班学生这次考试成绩的平均数为29.4分 C、该班学生这次考试成绩的众数为30分 D、该班学生这次考试成绩的中位数为28分7. 如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则 : 的值为 A、1:3 B、1:5 C、1:6 D、1:118. 现有四张完全相同的卡片,上面分别标有数字0,1,2,3,把卡片背面朝上洗匀,然后从中随机抽取两张卡片组成一个两位数,则这个两位数是偶然的概率是( )A、 B、 C、 D、9. 如图,在 中, , ,分别以点A和点C为圆心,大于 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则 的度数为
A、1:3 B、1:5 C、1:6 D、1:118. 现有四张完全相同的卡片,上面分别标有数字0,1,2,3,把卡片背面朝上洗匀,然后从中随机抽取两张卡片组成一个两位数,则这个两位数是偶然的概率是( )A、 B、 C、 D、9. 如图,在 中, , ,分别以点A和点C为圆心,大于 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则 的度数为 A、 B、 C、 D、10. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是
A、 B、 C、 D、10. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是 A、
A、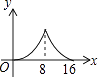 B、
B、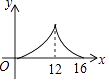 C、
C、 D、
D、
二、填空题
-
11. 计算: .12. 不等式组 的最大整数解为 .13. 如图,A,B是反比例函数 图象上的两点,过点A作 轴,垂足为C,AC交OB于点 若D为OB的中点, 的面积为6,则k的值为
 14. 如图,在扇形OAB中,C是OA的中点, ,CD与 交于点D,以O为圆心,OC的长为半径作 交OB于点E,若 , ,则图中阴影部分的面积为 结果保留
14. 如图,在扇形OAB中,C是OA的中点, ,CD与 交于点D,以O为圆心,OC的长为半径作 交OB于点E,若 , ,则图中阴影部分的面积为 结果保留 15. 如图,在矩形ABCD中, , ,点E为射线DC上一个动点,把 沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .
15. 如图,在矩形ABCD中, , ,点E为射线DC上一个动点,把 沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .
三、解答题
-
16. 先化简,再求值: ,其中 .17. 如图,一次函数 与反比例函数 的图象交于 , 两点.
 (1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式 的解集;(3)、过点B作 轴,垂足为C,求 的面积.18. 每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式 的解集;(3)、过点B作 轴,垂足为C,求 的面积.18. 每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: (1)、此次抽样调查的样本容量是 ;(2)、补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;(3)、如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?19. 如图,AB是 的一条弦,E是AB的中点,过点E作 于点C,过点B作 的切线交CE的延长线于点D.
(1)、此次抽样调查的样本容量是 ;(2)、补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;(3)、如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?19. 如图,AB是 的一条弦,E是AB的中点,过点E作 于点C,过点B作 的切线交CE的延长线于点D. (1)、求证: ;(2)、若 , ,求 的半径.20. 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为 ,在楼顶C测得塔顶A的仰角为 若小山高 ,楼的底部D与山脚在同一水平面上,求铁塔的高 参考数据: ,
(1)、求证: ;(2)、若 , ,求 的半径.20. 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为 ,在楼顶C测得塔顶A的仰角为 若小山高 ,楼的底部D与山脚在同一水平面上,求铁塔的高 参考数据: , 21. 由于数学课上需要用到科学计算器,班级决定集体购买,班长小明先去文具店购买了2个A型计算器和3个B型计算器,共花费90元;后又买了1个A型计算器和2个B型计算器,共花费55元(每次两种计算器的售价都不变)(1)、求A型计算器和B型计算器的售价分别是每个多少元?(2)、经统计,班内还需购买两种计算器共40个,设购买A型计算器t个,所需总费用w元,请求出w关于t的函数关系式;(3)、要求:B型计算器的数量不少于A型计数器的2倍,请设计一种购买方案,使所需总费用最低.22. 如图1,过等边三角形ABC边AB上一点D作 交边AC于点E,分别取BC,DE的中点M,N,连接MN.
21. 由于数学课上需要用到科学计算器,班级决定集体购买,班长小明先去文具店购买了2个A型计算器和3个B型计算器,共花费90元;后又买了1个A型计算器和2个B型计算器,共花费55元(每次两种计算器的售价都不变)(1)、求A型计算器和B型计算器的售价分别是每个多少元?(2)、经统计,班内还需购买两种计算器共40个,设购买A型计算器t个,所需总费用w元,请求出w关于t的函数关系式;(3)、要求:B型计算器的数量不少于A型计数器的2倍,请设计一种购买方案,使所需总费用最低.22. 如图1,过等边三角形ABC边AB上一点D作 交边AC于点E,分别取BC,DE的中点M,N,连接MN. (1)、发现:在图1中, ;(2)、应用:如图2,将 绕点A旋转,请求出 的值;(3)、拓展:如图3, 和 是等腰三角形,且 ,M,N分别是底边BC,DE的中点,若 ,请直接写出 的值.23. 如图,抛物线 的对称轴是直线 ,与x轴交于A,B两点,与y轴交于点C,点A的坐标为 ,点P为抛物线上的一个动点,过点P作 轴于点D,交直线BC于点E.
(1)、发现:在图1中, ;(2)、应用:如图2,将 绕点A旋转,请求出 的值;(3)、拓展:如图3, 和 是等腰三角形,且 ,M,N分别是底边BC,DE的中点,若 ,请直接写出 的值.23. 如图,抛物线 的对称轴是直线 ,与x轴交于A,B两点,与y轴交于点C,点A的坐标为 ,点P为抛物线上的一个动点,过点P作 轴于点D,交直线BC于点E. (1)、求抛物线解析式;(2)、若点P在第一象限内,当 时,求四边形POBE的面积;(3)、在 的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线解析式;(2)、若点P在第一象限内,当 时,求四边形POBE的面积;(3)、在 的条件下,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B,D,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,请说明理由.