河南省南阳市方城县2018届数学中考一模试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. 下列各数中,比﹣ 小的数是( )A、﹣1 B、 C、 D、02. 近期浙江大学的科学家们研制出今为止世界上最轻的材料,这种被称为“全碳气凝胶”的固态材料密度仅每立方厘米0.00016克,数据0.00016用科学记数法表示应是( )A、1.6×104 B、0.16×10﹣3 C、1.6×10﹣4 D、16×10﹣53. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在正方体的一角截去一个小正方体,所得立体图形的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=27°,则∠2的度数是( )
5. 如图,直线a∥b,Rt△ABC的直角顶点B落在直线a上,若∠1=27°,则∠2的度数是( ) A、53° B、63° C、73° D、83°6. 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )
A、53° B、63° C、73° D、83°6. 如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )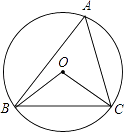 A、4 B、3 C、2 D、7. 不等式组 的解集是( )A、x>2 B、x≥3 C、2<x≤3 D、x≥28.
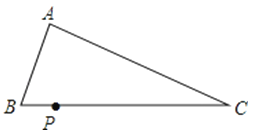
A、4 B、3 C、2 D、7. 不等式组 的解集是( )A、x>2 B、x≥3 C、2<x≤3 D、x≥28.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
 A、
A、 B、
B、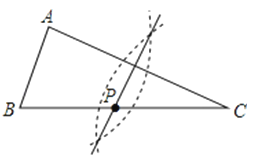 C、
C、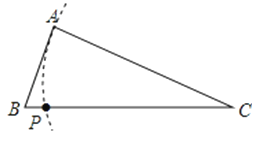 D、
D、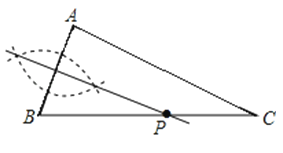 9. 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移一个单位”为一次变换.如此这样,连续经过2018次变换后,正方形ABCD的对角线交点M的坐标为( )
9. 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移一个单位”为一次变换.如此这样,连续经过2018次变换后,正方形ABCD的对角线交点M的坐标为( ) A、(2018,2) B、(2018,﹣2) C、(﹣2016,2) D、(2016,2)10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A、(2018,2) B、(2018,﹣2) C、(﹣2016,2) D、(2016,2)10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( ) A、
A、 B、
B、 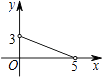 C、
C、 D、
D、
二、填空题
-
11. 计算:2cos60°﹣( +1)0= .12. 一副三角尺按如图的位置摆放(顶点C 与F 重合,边CA与边FE叠合,顶点B、C、D在一条直线上).将三角尺DEF绕着点F按顺时针方向旋转n°后(0<n<180 ),如果EF∥AB,那么n的值是 .
 13. 在一个不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机摸出一个球恰好是黄球的概率是 .则n= .14. 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°,CD是⊙O的切线:若⊙O的半径为2,则图中阴影部分的面积为 .
13. 在一个不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机摸出一个球恰好是黄球的概率是 .则n= .14. 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°,CD是⊙O的切线:若⊙O的半径为2,则图中阴影部分的面积为 . 15. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为 .
15. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为 .
三、解答题
-
16. 先化简,再求值: ,其中m= ﹣117. 某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
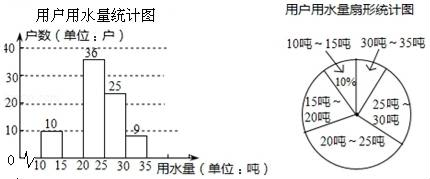 (1)、此次抽样调查的样本容量是
(1)、此次抽样调查的样本容量是
(2)、补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
18. 如图,已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F,连接AO并延长到点C,使OC=AO,连接CD、CB. (1)、试判断四边形ABCD的形状,并说明理由;(2)、若AB=4cm,填空:
(1)、试判断四边形ABCD的形状,并说明理由;(2)、若AB=4cm,填空:①当⊙O的半径为cm时,△ABD为等边三角形;
②当⊙O的半径为cm时,四边形ABCD为正方形.
19. 如图,某兴趣小组用高为1.6米的仪器测量塔CD的高度.由距塔CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为10米,tanα=1.6,tanβ=1.2,试求塔CD的大约高度. 20. 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y= (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2 ,点A的纵坐标为4.
20. 如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y= (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2 ,点A的纵坐标为4. (1)、求该反比例函数和一次函数的解析式;(2)、连接MC,求四边形MBOC的面积.21. 某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)、求该反比例函数和一次函数的解析式;(2)、连接MC,求四边形MBOC的面积.21. 某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)、求购进甲、乙两种纪念品每件各需多少元?(2)、若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案?
(3)、若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?22. 如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立. (1)、当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(1)、当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=3 时,求线段DH的长.
23. 如图,已知二次函数y= x2+bx﹣ 与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E. (1)、试求出二次函数的表达式和点B的坐标;(2)、当点P在线段AO(点P不与A、O重合)运动至何处时,线段OE的长有最大值,求出这个最大值;(3)、是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
(1)、试求出二次函数的表达式和点B的坐标;(2)、当点P在线段AO(点P不与A、O重合)运动至何处时,线段OE的长有最大值,求出这个最大值;(3)、是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.