河南省洛阳市2018届数学中招模拟试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
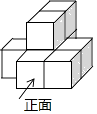
1. 在实数0,-1.5,1,- 中,比-2小的数是( )A、0 B、-1.5 C、1 D、-2. 据统计,2017年,我国国内生产总值达到82.7万亿元,数据“82.7万亿”用科学记数法表示为( )A、82.7×1012 B、8.27×1013 C、8.27×1012 D、82.7×10133. 下列运算正确的是( )A、 - = B、(-3)2=6 C、3a4-2a2=a2 D、(-a3)2=a54. 如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 把不等式组 的解集表示在数轴上,下列不符合题意的是( )A、
5. 把不等式组 的解集表示在数轴上,下列不符合题意的是( )A、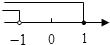 B、
B、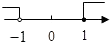 C、
C、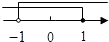 D、
D、 6. 某校九年级(1)班全体学生进行体育测试的成绩(满分70分)统计如表:根据表中的信息判断,下列结论中错误的是( )
6. 某校九年级(1)班全体学生进行体育测试的成绩(满分70分)统计如表:根据表中的信息判断,下列结论中错误的是( )成绩(分)
45
50
55
60
65
68
70
人数(人)
2
6
10
7
6
5
4
A、该班一共有40名同学 B、该班学生这次测试成绩的众数是55分 C、该班学生这次测试成绩的中位数是60分 D、该班学生这次测试成绩的平均数是59分7. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) A、2 B、 C、 D、8. 关于x的一元二次方程(a-5)x2-4x-1=0有实数根,则a满足( )A、a≥1且a≠5 B、a>1且a≠5 C、a≥1 D、a>19. 如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=- (x<0)的图像交与点C,若BA∶AC=2∶1,则a的值为( )
A、2 B、 C、 D、8. 关于x的一元二次方程(a-5)x2-4x-1=0有实数根,则a满足( )A、a≥1且a≠5 B、a>1且a≠5 C、a≥1 D、a>19. 如图,平面直角坐标系中,直线y=-x+a与x、y轴的正半轴分别交于点B和点A,与反比例函数y=- (x<0)的图像交与点C,若BA∶AC=2∶1,则a的值为( ) A、-3 B、-2 C、3 D、210. 如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )
A、-3 B、-2 C、3 D、210. 如图,P是菱形ABCD的对角线AC上一动点,过P作垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
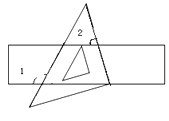
11. 计算: =12. 如图,把一块等腰直角三角形的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2是度.
 13. 如图是两个质地均匀的转盘,现转动转盘①和转盘②各一次,则两个转盘指针都指向红的部分的概率为.
13. 如图是两个质地均匀的转盘,现转动转盘①和转盘②各一次,则两个转盘指针都指向红的部分的概率为.
 14. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的中点,D是OA的中点,则图中阴影部分的面积为cm2.
14. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的中点,D是OA的中点,则图中阴影部分的面积为cm2. 15. 如图在菱形ABCD中,∠A=60°,AD= ,点P是对角线AC上的一个动点,过点P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为.
15. 如图在菱形ABCD中,∠A=60°,AD= ,点P是对角线AC上的一个动点,过点P作EF⊥AC交AD于点E,交AB于点F,将△AEF沿EF折叠点A落在G处,当△CGB为等腰三角形时,则AP的长为.
三、解答题
-
16. 先化简再求值 (a+2b)(a-2b)-(a-b)2+5b(a+b),其中a=2- ,b=2+ .17. 中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分
频数
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25

请根据所给信息,解答下列问题:
(1)、m= , n=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
18. 如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.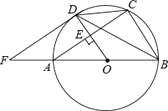 (1)、求证:FD是⊙O的切线;(2)、若⊙O的半径为5,sinF= ,求DF的长。
(1)、求证:FD是⊙O的切线;(2)、若⊙O的半径为5,sinF= ,求DF的长。
19. 如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)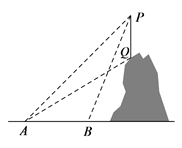 20. 如图,在平面直角坐标系中,A点的坐标是(3,3),AB⊥x轴于点B,反比例函数y= 的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
20. 如图,在平面直角坐标系中,A点的坐标是(3,3),AB⊥x轴于点B,反比例函数y= 的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM. (1)、求反比例函数的解析式;(2)、若直线MN交y轴于点C,求△OMC的面积。
(1)、求反比例函数的解析式;(2)、若直线MN交y轴于点C,求△OMC的面积。
21. 某通讯运营商的手机上网流量资费标准推出了三种优惠方案:方案A:按流量计费,0.1元/M;

方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)、写出方案A的函数解析式,并在图中画出其图象;(2)、直接写出方案B的函数解析式;
(3)、若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.22. 在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D是AB边上的中点,Rt△EFG的直角顶点E在AB边上移动.

 (1)、如图1,若点D与点E重合且EG⊥AC、DF⊥BC,分别交AC、BC于点M、N,
(1)、如图1,若点D与点E重合且EG⊥AC、DF⊥BC,分别交AC、BC于点M、N,易证EM=EN;如图2,若点D与点E重合,将△EFG绕点D旋转,则线段EM与EN的长度还相等吗?若相等请给出证明,不相等请说明理由;
(2)、将图1中的Rt△EGF绕点D顺时针旋转角度α(0∘<α<45∘). 如图2,在旋转过程中,当∠MDC=15∘时,连接MN,若AC=BC=2,请求出线段MN的长;
(3)、图3, 旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合),当AB=3AE时,线段EM与EN的数量关系是;当AB=m·AE时,线段EM与EN的数量关系是.
23. 如图,在平面直角坐标系中,一次函数y=− x+2的图象与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c关于直线x= 对称,且经过B. C两点,与x轴交于另一点为A. (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、若点P为直线AC上方的抛物线上的一点,过点P作PQ⊥x轴于M,交AC于Q,求PQ的最大值,并求此时△APC的面积;
(3)、在抛物线的对称轴上找出使△ADC为直角三角形的点D,直接写出点D的坐标.