广东省深圳市福田区2018届九年级下学期教学质量检测数学试卷

试卷更新日期：2018-09-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果“收入10元”记作作+10元，那么支出20元记作（）

A、+20 B、-20元 C、+10元 D、-10元

查看试题解析
2. 如图所示的圆锥体的三视图中，是中心对称图形的是（）

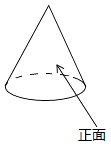A、主视图 B、左视图 C、俯视图 D、以上答案都不对

查看试题解析
3. 2017年，粤港澳大湾区发展取得显著成效，全年GDP将达到1.4万亿美元，经济总量有望在未来几年超越美国纽约湾区，成为全球第二大湾区；1.4万亿美元用科学记数法表示为（）

A、 1.4×10³亿美元 B、1.4×10⁴亿美元 C、1.4×10⁸亿美元 D、1.4×10¹²亿美元

查看试题解析
4. 下列运算正确的是（）

A、2a+3a=5a B、(x-2)²=x²-4 C、(x-2)(x-3)=x²-6 D、a⁸÷a⁴=a²

查看试题解析
5. 我市某小区开展了“节约用水为环保做贡献”的活动，为了解居民用水情况，在小区随机抽查了10户家庭的月用水量，结果如下表
月用水量（吨）
8
9
10
户数
2
6
2
则关于这10户家庭的月用水量，下列说法错误的是（）

A、方差是4 B、极差2 C、平均数是9 D、众数是9

查看试题解析
6. 下列说法中正确的是（）

A、8的立方根是2 B、函数y= $\frac{1}{x - 1}$ 的自变量x的取值范围是x>1 C、同位角相等 D、两条对角线互相垂直的四边形是菱形

查看试题解析
7. 如图，函数y=2x和y= $\frac{2}{x}$ (x>0))的图象相交于点A（m，2），观察图象可知，不等式 $\frac{2}{x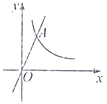}$ <2x的解集为（）

A、x<0 B、x>1 C、0<x<1 D、0<x<2

查看试题解析
8. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

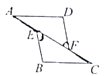A、∠A=∠C B、AD∥BC C、BE=DF D、AD=CB

查看试题解析
9. 如图，线段CD的两个端点的坐标分别为C(1，2)，D(2，0)，以原点为位似中心，将线段CD放大得到线段AB，若点B的坐标为(5，0)，则点A的坐标为（）

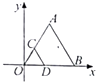A、(2，5) B、(3，6) C、(3，5) D、(2.5，5)

查看试题解析
10. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为 $570 m^{2}$ ，若设道路的宽为 $x m$ ，则下面所列方程正确的是（）

A、(32-2x)(20-x)=570 B、32x+2×20x=32×20-570 C、(32-x)(20-x)=32×20-570 D、32x+2×20x-2x²=570

查看试题解析
11. 如图，在△ABC中，∠ACB=90°，按如下步骤操作：①以点A为圆心，任意长为半径作弧，分别交AC、AB于D、E两点；②以点C为圆心，AD长为半径作弧，交.AC的延长线于点F；③以点F为圆心，DE长为半径作弧，两弧交于点G；④作射线CG，若∠FCG=50°，则∠B为（）

A、30° B、40° C、50° D、60°

查看试题解析
12. 如图，在平面直角坐标系中，正方形ABCO的边长为3，点O为坐标原点，点A、C分别在x轴、y轴上，点B在第一象限内直线y=kx+1分别与x轴、y轴、线段BC交于点F、D、G，AE⊥FG，下列结论：①△GCD和△FOD的面积比为3：1：②AE的最大长度为 $\sqrt{10}$ ：③tan∠FEO= $\frac{1}{3}$ ④当DA平分∠EAO时，CG= $\frac{3}{2}$ ，其中正确的结论有（）

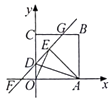A、①②③ B、②③ C、②③④ D、③④

查看试题解析

二、填空题

13. 分解因式： $ab - b^{2} =$ .

查看试题解析
14. 在一个不透明的空袋子里，放入仅颜色不同的2个红球和1个白球，从中随机摸出1个球后不放回，再从中随机摸出1个球，两次都摸到红球的概率是．

查看试题解析
15. 对于实数a、b，定义一种运算“ $@$ ”为： $a @ b = a^{2} + a b - 1$ .若 $x @ 2 = 0 ，$ 则 $2 x^{2} + 4 x - 3 =$ .

查看试题解析
16. 如图，四边形OABC中，AB∥OC，边OA在x轴的正半轴上，OC在y轴的正半轴上，点B在第一象限内，点D为AB的中点，CD与OB相交于点E，若△BDE、△OCE的面积分别为1和9，反比例函数y= $\frac{k}{x}$ 的图象经过点B，则k=.

查看试题解析

三、解答题

17. 计算： ${\frac{1}{2}}^{- 1} - 6 tan 30 ° + 2 - {\sqrt{2}}^{0} + \sqrt{12}$

查看试题解析
18. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div （ 1 + \frac{2}{a - 1} ）$ ，其中a=-1

查看试题解析
19. 深圳市某校艺术节期间，开展了“好声音”歌唱比赛，在初赛中，学生处对初赛成绩做了统计分析，绘制成如下频数、频率分布直方图（如图），请你根据图表提供的信息，解答下列问题：

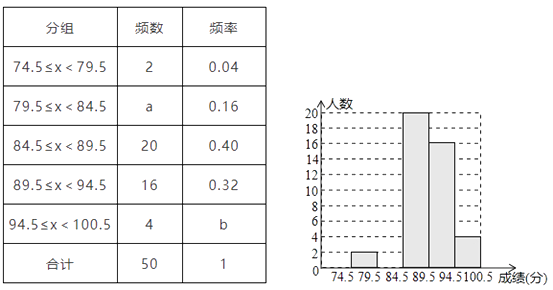(1)、频数、频率分布表中a= ， b=；

(2)、补全频数分布直方图；

(3)、初赛成绩在94.5≤x＜100.5分的四位同学恰好是七年级、八年级各一位，九年级两位，学生处打算从中随机挑选两位同学谈一下决赛前的训练，则所选两位同学恰好都是九年级学生的概率为

查看试题解析
20. 矗立在莲花山的邓小平雕像气宇轩昂，这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°，点D的仰角∠DBC=30°，已知CD=2米，求像体AD的高度。（最后结果精确到1米，参考数据：sin67°≈0.92，cos67°≈0.39，tan67°≈2.4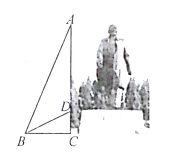， $， \sqrt{3}$ ≈1.7）

查看试题解析
21. 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

(1)、求y与x之间的函数关系式；

(2)、当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

查看试题解析
22. 如图，在平面内直角坐标系中，直线y=-x+6分别于x轴、y轴交于A、B两点，点C与点A关于y轴对称，点E为线段OB上一动点（不与O、B重合），CE的延长线与AB交于点D，过A、D、E三点的圆与y轴交于点F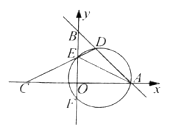

(1)、求A、B、C三点的坐标

(2)、求证：BE·EF=DE·AE

(3)、若tan∠BAE= $\frac{1}{3}$ ，求点F的坐标

查看试题解析
23. 已知抛物线y=a(x-2)²-9经过点P(6，7)，与x轴交于A、B两点，与y轴交于点C，直线AP与y轴交于点D，抛物线对称轴与x轴交于点E.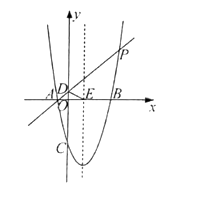

(1)、求抛物线的解析式；

(2)、过点E任作一条直线l(点B、C分别位于直线l的异侧)，设点C到直线的距离为m，点B到直线l的距离为n，求m+n的最大值；

(3)、y轴上是否存在点Q，使∠QPD=∠DEO，若存在，请求出点Q的坐标：若不存在，请说明理由.

查看试题解析

月用水量（吨）	8	9	10
户数	2	6	2