广东省深圳市福田片区2018届九年级24校联考数学试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. -2相反数是( )A、 B、-2 C、2 D、-2. 如图所示的几何体中,从上面看到的图形相同的是( )
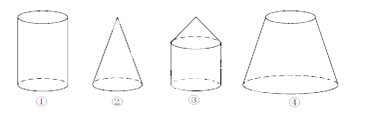 A、①② B、①③ C、②③ D、②④3. 为响应国家的新能源政策,深圳市某公司计划在海边建设风能发电站,电站年均发电量约为 216000000 度,将数据 216000000 用科学记数法表示为( )A、216×10 6 B、21.6×10 7 C、2.16×10 8 D、2.16×10 94. 下列运算正确的是( )A、a+b=ab B、a2·a3=a6 C、a2+2ab-b2= (a+b)2 D、3a-2a=a5. 某商品的标价为 300 元,打 8 折销售仍可获利 20%,则商品进价为( )元.A、140 B、120 C、160 D、2006. 四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A、①② B、①③ C、②③ D、②④3. 为响应国家的新能源政策,深圳市某公司计划在海边建设风能发电站,电站年均发电量约为 216000000 度,将数据 216000000 用科学记数法表示为( )A、216×10 6 B、21.6×10 7 C、2.16×10 8 D、2.16×10 94. 下列运算正确的是( )A、a+b=ab B、a2·a3=a6 C、a2+2ab-b2= (a+b)2 D、3a-2a=a5. 某商品的标价为 300 元,打 8 折销售仍可获利 20%,则商品进价为( )元.A、140 B、120 C、160 D、2006. 四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )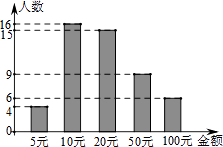 A、20,10 B、10,20 C、16,15 D、15,167. 如图,点P在△ABC的边AC上,添加以下一个条件,不能判断△ABP∽△ACB的是( )
A、20,10 B、10,20 C、16,15 D、15,167. 如图,点P在△ABC的边AC上,添加以下一个条件,不能判断△ABP∽△ACB的是( )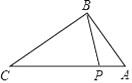 A、∠ABP=∠C B、∠APB=∠ABC C、 D、8. 某单位向一所希望小学赠送1080 件文具,现用 A,B 两种不同的包装箱进行包装,已知每个B型包装箱比 A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为( )
A、∠ABP=∠C B、∠APB=∠ABC C、 D、8. 某单位向一所希望小学赠送1080 件文具,现用 A,B 两种不同的包装箱进行包装,已知每个B型包装箱比 A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为( )
A、 B、 C、 D、9. 已知点 A(x1 , y1),B(x2 , y2 )是反比例函数 的图象上的两点,若 x1<0<x2 , 则有( )
A、y1<0<y2 B、y2<0<y1 C、y1<y2<0 D、y2<y1<010. 如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )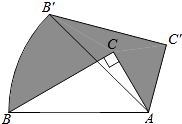 A、 B、 C、 D、π11. 如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
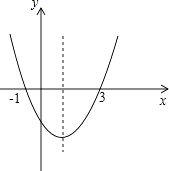
A、 B、 C、 D、π11. 如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
 A、1 B、2 C、3 D、412. Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB,AC 交于 E,F 两点.下列结论:① BE+CF= BC;② S△AEF ≤ S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
A、1 B、2 C、3 D、412. Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB,AC 交于 E,F 两点.下列结论:① BE+CF= BC;② S△AEF ≤ S△ABC;③ S四边形AEDF=AD•EF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )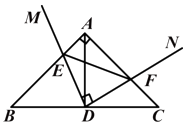 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 分解因式:3a3-3a= .14. 在△ABC中,若|cosA- |+(1-tanB)2=0,则∠C的度数是.
15. 设函数y= 与y=x-1的图象的交点坐标为(a,b),则 的值为.
16. 两个反比例函数y= ,y= 在第一象限内的图象如图所示,点P1 , P2 , P3 , ....,P99 , 在反比例函数y= 图象上,它们的横坐标分别是x1 , x2 , x3 , ....,x99 , 纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1 , P2 , P3 , …,P99分别作y轴的平行线线,与y= 的图象交点依次是Q1(x1 , y1),Q2(x2 , y2),Q3(x3 , y3),.....,Q99(x99 , y99),则y99=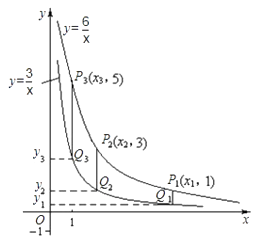
三、解答题
-
17. 计算( )-1 -tan 60° + -|1- |18. 先化简 ,然后从0,1,2中选择一个适当的数作为x的值代入求值。19. 为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:
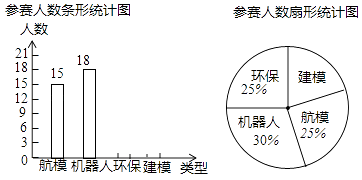
请根据以上信息,解答下列问题:
(1)、全体参赛的学生共有人,“建模”在扇形统计图中的圆心角是°;
(2)、将条形统计图补充完整;
(3)、在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?20. 如图,在Rt△ABC中,∠BAC= 90º,D是BC的中点,E是AD的中点,过点A作AF//BC 交 BE的延长线于点F,连接CF. (1)、求证:AD=AF.(2)、当AB=AC= 时,求四边形ADCF 的面积.21. 天虹超市购进甲、乙两种水果,已知 1 千克甲种水果的进价比 1 千克乙种水果的进价多 4 元,购进 2千克甲种水果与 3 千克乙种水果共需 28 元.
(1)、求证:AD=AF.(2)、当AB=AC= 时,求四边形ADCF 的面积.21. 天虹超市购进甲、乙两种水果,已知 1 千克甲种水果的进价比 1 千克乙种水果的进价多 4 元,购进 2千克甲种水果与 3 千克乙种水果共需 28 元.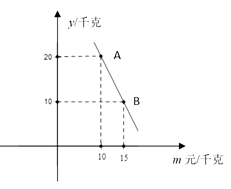 (1)、求甲种水果的进价为每千克多少元?
(1)、求甲种水果的进价为每千克多少元?
(2)、经市场调查发现,甲种水果每天销售量 y(千克)与售价 m(元/千克)之间满足如图所示的函数关系,求 y与 m 之间的函数关系;
(3)、在(2)的条件下,为减少库存,每天甲种水果的销售量不能低于 16 千克,当甲种水果的售价定为多少元时,才能使每天销售甲种水果的利润最大?最大利润是多少?
22. 如图,在△ABC 中,AB=AC,AE 是∠BAC 的平分线,∠ABC 的平分线 BM 交 AE 于点 M,点 O在 AB 上,以点O 为圆心,OB 的长为半径的圆经过点 M,交 BC 于点G,交 AB 于点 F.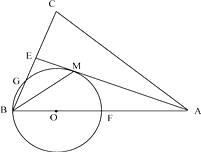 (1)、求证:AE 为⊙O 的切线.
(1)、求证:AE 为⊙O 的切线.
(2)、当 BC=8,AC=12 时,求⊙O 的半径.(3)、在(2)的条件下,求线段 BG 的长.
23. 如图,直线y=kx+3经过点B(- ,2),且与 x 轴交于点A.将抛物线 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P. (1)、求∠OAB 的度数;(2)、抛物线 与直线 y=kx+3相交于 M,N两点,求△MON的面积.(3)、在抛物线 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
(1)、求∠OAB 的度数;(2)、抛物线 与直线 y=kx+3相交于 M,N两点,求△MON的面积.(3)、在抛物线 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.