广东省汕尾市海丰县2018届数学中考模拟试卷

试卷更新日期：2018-09-30 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、4

查看试题解析
2. 作为世界文化遗产的长城，其总长大约为6700000m．将6700000用科学记数法表示为（）

A、6.7×10⁵ B、6.7×10⁶ C、0.67×10⁷ D、67×10⁸

查看试题解析
3.
如图，直线l与直线a ， b相交，且a∥b ， ∠1=110º，则∠2的度数是（）

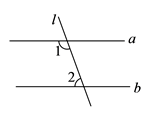A、20° B、70° C、90° D、110°

查看试题解析
4. 若关于x的不等式组的解表示在数轴上如图所示，则这个不等式组的解集是（）

A、x≤2 B、x＞1 C、1≤x＜2 D、1＜x≤2

查看试题解析
5. 某校10名篮球运动员的年龄情况，统计如下表：
年龄/岁
12
13
14
15
人数/名
2
4
3
1
则这10名篮球运动员年龄的中位数为（）

A、12 B、13 C、13.5 D、14

查看试题解析
6. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、等边三角形 B、干行四边形 C、正六边形 D、圆

查看试题解析
7. 已知：如图，菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD=6cm，则OE的长为（）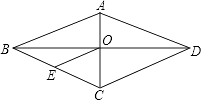

A、6cm B、4cm C、3cm D、2cm

查看试题解析
8. 下列运算正确的是（）

A、（a³）²=a⁵ B、a²•a³=a⁵ C、a⁶÷a²=a³ D、3a²﹣2a²=1

查看试题解析
9. 如图，已知：在⊙O中，OA⊥BC，∠AOB=70°，则∠ADC的度数为（）

A、70° B、45° C、35° D、30°

查看试题解析
10. 已知b>0时，二次函数y＝ax²＋bx＋a²－1的图象如下列四个图之一所示．
根据图分析，a的值等于（）

A、－2 B、－1 C、1 D、2

查看试题解析

二、填空题

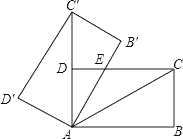
11. 分解因式：mn²-2mn+m=

查看试题解析
12. 一个正多边形的一个外角为30°，则它的内角和为．

查看试题解析
13. 若2x﹣3y﹣1=0，则5﹣4x+6y的值为．

查看试题解析
14. 某校共有学生1600人，为了解学生最喜欢的课外体育运动项目的情况，学校随机抽查了200名学生，其中有85名学生表示最喜欢的项目是足球，则可估计该校学生中最喜欢的课外体育运动项目为足球的学生有人．

查看试题解析
15. 已知扇形的圆心角为120°，弧长为6π，则扇形的面积是．

查看试题解析
16. 如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC′的中点恰好与D点重合，AB′交CD于点E．若AB=6，则△AEC的面积为．

查看试题解析

三、解答题

17. 计算：2sin60°+|3﹣ $\sqrt{3}$ |﹣（ $\frac{1}{2}$ ）^﹣¹+（π﹣2018）⁰

查看试题解析
18. 先化简，再求值： $\frac{x}{x + 2}$ ﹣ $\frac{1}{x - 1}$ ÷ $\frac{x + 2}{x^{2} - 2 x + 1}$ ，其中x=﹣3．

查看试题解析
19. 为进一步促进义务教育均衡发展，某县加大了基础教育经费的投入，已知2015年该县投入基础教育经费5000万元，2017年投入基础教育经费7200万元．求该县这两年投入基础教育经费的年平均增长率．

查看试题解析
20. 如图，已知在△ABC中，∠A=90°

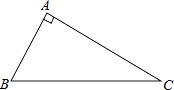(1)、请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．

(2)、若∠B=60°，AB=3，求⊙P的面积．

查看试题解析
21. 如图△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB．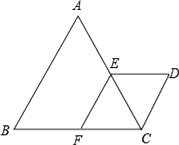

(1)、求证：四边形EFCD是菱形；

(2)、设CD=4，求D、F两点间的距离．

查看试题解析
22. 端午节吃粽子是中华民族的传统习惯．农历五月初五早晨，小王的妈妈用不透明袋子装着一些粽子（粽子除食材不同外，其他一切相同），其中糯米粽两个，还有一些薯粉粽，现小王从中任意拿出一个是糯米粽的概率为 $\frac{1}{2}$ ．

(1)、求袋子中薯粉粽的个数；

(2)、小王第一次任意拿出一个粽子（不放回），第二次再拿出一个粽子，请你用树形图或列表法，求小王两次拿到的都是薯粉粽的概率．

查看试题解析
23. 如图，已知函数 $y = \frac{k}{x}$ （x>0）的图象经过点A，B，点A的坐标为(1，2)．过点A作AC∥y轴，AC＝1（点C位于点A的下方），过点C作CD∥x轴，与函数的图象交于点D，过点B作BE⊥CD，垂足E在线段CD上，连接OC，OD．

(1)、求△OCD的面积；

(2)、当BE＝ $\frac{1}{2}$ AC时，求CE的长．

查看试题解析
24. 如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P．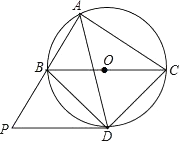

(1)、求证：PD是⊙O的切线；

(2)、求证：△PBD∽△DCA；

(3)、当AB=6，AC=8时，求线段PB的长．

查看试题解析
25. 如图所示，在平面直角坐标系中，抛物线y=ax²+bx+c经过A（-3，0）、B（1，0）、C（0，3）三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．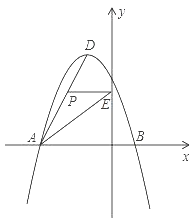

(1)、求抛物线的函数解析式，并写出顶点D的坐标；

(2)、如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值；

(3)、在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上．

查看试题解析

年龄/岁	12	13	14	15
人数/名	2	4	3	1