广东省汕头市龙湖区2018届数学中考模拟试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
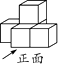
1. 5的倒数是( )A、-5 B、 C、 D、不存在2. 去年汕头市经济发展成绩斐然,全市投资总额首次突破200 000 000 000元,其中200 000 000 000用科学记数法表示为( )A、2×1012 B、0.2×1012 C、2×1011 D、20×10113. 如图是由五个相同的小正方块搭成的几何体,其左视图是( )
 A、
A、 B、
B、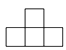 C、
C、 D、
D、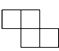 4. , , 三个数在数轴上的位置如图所示,则这三个数中绝对值最大的是( )
4. , , 三个数在数轴上的位置如图所示,则这三个数中绝对值最大的是( ) A、a B、b C、c D、无法确定5. 点 在反比例函数 的图象上,则 的值是( )
A、a B、b C、c D、无法确定5. 点 在反比例函数 的图象上,则 的值是( )
A、-10 B、5 C、-5 D、106. 某特警对为了选拔“神枪手”举行射击比赛,最后由甲、乙两名战士进入决赛,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人成绩的稳定性相同 D、无法确定谁的成绩更稳定7. 圆心角为 ,弧长为 的扇形半径为( )A、 B、 C、 D、8. 下列运算正确的是( )A、 B、 C、 D、9. 已知 ,则代数式 的值是( )
A、-3 B、0 C、3 D、610. 如图,四边形ABCD是正方形,点P,Q分别在边AB,BC的延长线上且BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②△OAE∽△OPA;③当正方形的边长为3,BP=1时,cos∠DFO= ,其中正确结论的个数是( )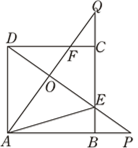 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
11. 在函数 中,自变量 的取值范围是 .12. 计算: = .13. 分式方程 的解为 .14. 已知一个正多边形的每个外角都等于45°,则这个正多边形的边数是 .15. 如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN=cm.
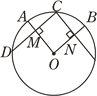 16. 如图,将矩形 绕点 旋转至矩形 位置,此时 的中点恰好与 点重合, 交 于点 .若 =1,则矩形 的面积为.
16. 如图,将矩形 绕点 旋转至矩形 位置,此时 的中点恰好与 点重合, 交 于点 .若 =1,则矩形 的面积为.
三、解答题
-
17. 计算题:18. 先化简,再求值: ,其中 -319. 某镇枇杷园的枇杷除了运往市区销售外,还可以让市民亲自去园内采摘购买,已知今年3月份该枇杷在市区、园内的销售价格分别为6元/千克、4元/千克,一共销售了3000千克,总销售额为16000元,3月份该枇杷在市区、园内各销售了多少千克?
20. 如图,在△ABC中,∠A=40°,∠C=60°.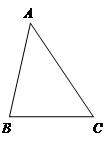 (1)、用直尺和圆规作∠ABC的平分线,交AC于D(保留作图痕迹,不要求写作法);(2)、在(1)的条件下,求∠BDC的度数.
(1)、用直尺和圆规作∠ABC的平分线,交AC于D(保留作图痕迹,不要求写作法);(2)、在(1)的条件下,求∠BDC的度数.
21. 如图,某商场为方便顾客使用购物车,准备将滚动电梯的坡面的倾斜角由45°降为30°,如果改动前电梯的坡面AB长为12米,点D、B、C在同一水平地面上.求改动后电梯水平宽度增加部分BC的长.(结果精确到0.1,参考数据: )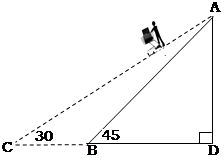 22. 某中学九年级(1)班为了了解全班学生的兴趣爱好情况,采取全面调查的方法,从舞蹈、书法、唱歌、绘画等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择其中一种自己喜欢的兴趣项目),请你根据图中提供的信息解答下列问题:
22. 某中学九年级(1)班为了了解全班学生的兴趣爱好情况,采取全面调查的方法,从舞蹈、书法、唱歌、绘画等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择其中一种自己喜欢的兴趣项目),请你根据图中提供的信息解答下列问题: (1)、九年级(1)班的学生人数为 , 并将图①中条形统计图补充完整 ;
(1)、九年级(1)班的学生人数为 , 并将图①中条形统计图补充完整 ;
(2)、图②中表示“绘画”的扇形的圆心角是度;(3)、“舞蹈”兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的舞蹈队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.23. 如图,抛物线y1=ax2+2ax+1与 轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.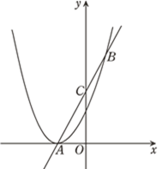 (1)、求 的值;
(1)、求 的值;
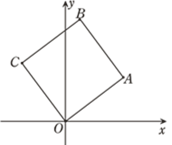
(2)、求直线AB对应的函数解析式;(3)、直接写出当y1 ≥y2 时, 的取值范围.24. 如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.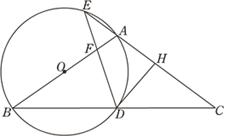 (1)、求证:DH是圆O的切线;(2)、若 ,求证:A为EH的中点.(3)、若EA=EF=1,求圆O的半径.25. 如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3).
(1)、求证:DH是圆O的切线;(2)、若 ,求证:A为EH的中点.(3)、若EA=EF=1,求圆O的半径.25. 如图,正方形OABC的顶点O在坐标原点,顶点A的坐标为(4,3).
(备用图)
(1)、顶点 的坐标为( , );(2)、现有动点P、Q分别从C、A同时出发,点P沿线段CB向终点B运动,速度为每秒1个单位,点Q沿折线A→O→C向终点C运动,速度为每秒k个单位,当运动时间为2秒时,以P、Q、C为顶点的三角形是等腰三角形,求此时k的值.(3)、若正方形OABC以每秒 个单位的速度沿射线AO下滑,直至顶点C落到 轴上时停止下滑.设正方形OABC在 轴下方部分的面积为S,求S关于滑行时间 的函数关系式,并写出相应自变量 的取值范围.