广东省汕头市濠江区2018届数学中考模拟试卷
试卷更新日期:2018-09-30 类型:中考模拟
一、单选题
-
1. 在实数0,﹣2, ,2中,最大的是( )A、0 B、﹣2 C、 D、22. 以下分别是回收、节水、绿色包装、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某篮球队10名队员的年龄如下表所示:
3. 某篮球队10名队员的年龄如下表所示:年龄(岁)
18
19
20
21
人数
2
4
3
1
则这10名队员年龄的众数和中位数分别是( )
A、19,19 B、19,19.5 C、20,19 D、20,19.54. 下列计算正确的是( )A、 B、 C、 D、5. 将一把直尺与一块三角板如图放置,若 ,则 为( )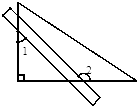 A、 B、 C、 D、6. 关于 的方程 的一个根为 ,则另一个根为( ).A、 B、 C、 D、7. 世界文化遗产长城总长约670000米,将数670000用科学记数法可表示为( )A、6.7×104 B、6.7×105 C、6.7×106 D、67×1048. 一元一次不等式组 的解集在数轴上表示出来,正确的是( )A、
A、 B、 C、 D、6. 关于 的方程 的一个根为 ,则另一个根为( ).A、 B、 C、 D、7. 世界文化遗产长城总长约670000米,将数670000用科学记数法可表示为( )A、6.7×104 B、6.7×105 C、6.7×106 D、67×1048. 一元一次不等式组 的解集在数轴上表示出来,正确的是( )A、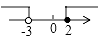 B、
B、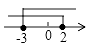 C、
C、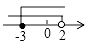 D、
D、 9. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
9. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )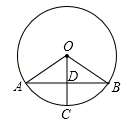 A、2 B、3 C、4 D、510. 如图,抛物线 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程 的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )
A、2 B、3 C、4 D、510. 如图,抛物线 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程 的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )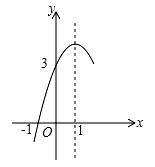 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 分解因式: .12. 函数 中自变量x的取值范围为 .13. 已知关于x的方程 有两个相等的实数根,那么m =14. 点P(-3, 4)关于y轴的对称点P′的坐标是15. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将Rt△ABC绕点A逆时针旋转30°后得到△ADE,则图中阴影部分的面积为
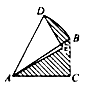
三、解答题
-
16. 计算:17. 先化简,再求值: ,其中x=2.18. 如图,在Rt△ABC中,∠BAC=90°.
 (1)、作∠ABC的平分线交AC边于点P, 再以点P为圆心,PA长为半径作⊙P
(1)、作∠ABC的平分线交AC边于点P, 再以点P为圆心,PA长为半径作⊙P(要求:尺规作图,保留作图痕迹,不写作法.);
(2)、请你判断(1)中BC与⊙P的位置关系:19. 小张和同学相约“五一”节到离家2400米的电影院看电影,到电影院后,发现电影票忘带了,此时离电影开始还有25分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回电影院,已知小张骑车的时间比跑步的时间少用了4分钟,骑车的平均速度是跑步的平均速度的1.5倍.
(1)、求小张跑步的平均速度;
(2)、如果小张在家取票和寻找“共享单车”共用了6分钟,他能否在电影开始前赶到电影院?说明理由.
20. 如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.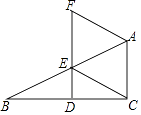 (1)、证明:AF=CE;
(1)、证明:AF=CE;
(2)、当∠B=30°时,试判断四边形ACEF的形状并说明理由.21. 中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.
请你根据统计图解答下列问题:
(1)、参加比赛的学生共有名;
(2)、在扇形统计图中,m的值为 , 表示“D等级”的扇形的圆心角为度;
(3)、组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
22. 如图,一次函数 (k≠0)的图象与反比例函数 (m≠0,x<0)的图象交于点A(-3,1)和点C,与y轴交于点B,△AOB的面积是6.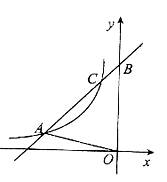 (1)、求一次函数与反比例函数的解析式;
(1)、求一次函数与反比例函数的解析式;
(2)、求 sin∠ABO的值;(3)、当x<0时,比较 与 的大小.
23. 如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F. (1)、判断DE与⊙O的位置关系,并说明理由;
(1)、判断DE与⊙O的位置关系,并说明理由;
(2)、若⊙O的半径R=5,tanC= ,求EF的长.24. 如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.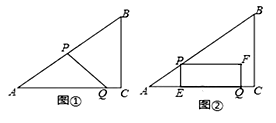 (1)、求线段AQ的长;(用含t的代数式表示)(2)、连结PQ,当PQ与△ABC的一边平行时,求t的值;(3)、如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF.设矩形PEQF与△ABC重叠部分图形的面积为S.直接写出点P在运动过程中S与t之间的函数关系式和自变量的取值范围.
(1)、求线段AQ的长;(用含t的代数式表示)(2)、连结PQ,当PQ与△ABC的一边平行时,求t的值;(3)、如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF.设矩形PEQF与△ABC重叠部分图形的面积为S.直接写出点P在运动过程中S与t之间的函数关系式和自变量的取值范围.