2018-2019学年数学浙教版八年级上册 第一章 三角形的初步知识 单元测试卷

试卷更新日期：2018-09-30 类型：单元试卷

进入 出卷网 下载

一、选择题

  • 1. 下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等．其中正确的是（   ）
    A、①② B、②③ C、①③ D、①②③

    查看试题解析

  • 2. 下列说法中，正确的个数是（   ）

    ①三角形的中线、角平分线、高都是线段；②三角形的三条角平分线、三条中线、三条高都在三角形内部；③直角三角形只有一条高；④三角形的三条角平分线、三条中线、三条高分别交于一点．

    A、1 B、2 C、3 D、4

    查看试题解析

  • 3. 如图，△ABC中，∠ABC，∠ACB的三等分线交于点E，D，若∠BFC=120°，∠BGC=102°，则∠A的度数为（   ）

    A、34° B、40° C、42° D、46°

    查看试题解析

  • 4. 如图，AE是△ABC的中线，已知EC=4，DE=2，则BD的长为（   ）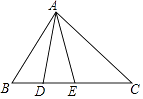

    A、2 B、3 C、4 D、6

    查看试题解析

  • 5. 如图，在△ABC中，∠ABC=40°，∠ACD=76°，BE平分∠ABC，CE平分△ABC的外角∠ACD，则∠E=（   ）

    A、40° B、36° C、20° D、18°

    查看试题解析

  • 6. 在△ABC和△DEF中，∠A=50°，∠B=70°，AB=3cm，∠D=50°，∠E=70°，EF=3cm．则△ABC与△DEF（   ）
    A、一定全等 B、不一定全等 C、一定不全等 D、不确定

    查看试题解析

  • 7. 如图，有一△ABC，今以B为圆心，AB长为半径画弧，交BC于D点，以C为圆心，AC长为半径画弧，交BC于E点．若∠B=40°，∠C=36°，则关于AD、AE、BE、CD的大小关系，下列何者正确？（   ）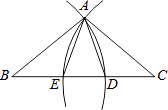

    A、AD=AE B、AD＜AE C、BE=CD D、BE＜CD

    查看试题解析

  • 8. 已知：如图，在△ABC中，边AB的垂直平分线分别交BC、AB于点G、D，若△AGC的周长为31cm，AB=20cm，则△ABC的周长为（    ）

    A、31cm B、41cm C、51cm D、61cm

    查看试题解析

  • 9. 如图，△ABC中，AD是BC边上的高，AE、BF分别是∠BAC、∠ABC的平分线，∠BAC=50°，∠ABC=60°，则∠EAD+∠ACD=（   ）

    A、75° B、80° C、85° D、90°

    查看试题解析

  • 10. 如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（   ）

    A、①②③ B、①③④ C、①④ D、①②④

    查看试题解析

二、填空题

  • 11. 已知一个等腰三角形的两边长分别是2和5，那么这个等腰三角形的周长为 ．

    查看试题解析

  • 12. 在△ABC中，∠ABC=100°，∠ACB=20°，CE平分∠ACB交AB于E，D在AC上，且∠CBD=20°，则∠CED的度数是 ．

    查看试题解析

  • 13. 如图，把一个三角尺的直角顶点D放置在△ABC内，使它的两条直角边DE，DF分别经过点B，C，如果∠A=30°，则∠ABD+∠ACD= ．

    查看试题解析

  • 14. 在学习“用直尺和圆规作射线OC，使它平分∠AOB”时，教科书介绍如下：*作法：

    ①以O为圆心，任意长为半径作弧，交OA于D，交OB于E；

    ②分别以D，E为圆心，以大于 12 DE的同样长为半径作弧，两弧交于点C；

    ③作射线OC．

    则OC就是所求作的射线．

    小明同学想知道为什么这样做，所得到射线OC就是∠AOB的平分线．

    小华的思路是连接DC、EC，可证△ODC≌△OEC，就能得到∠AOC=∠BOC．其中证明△ODC≌△OEC的理由是 ．

    查看试题解析

  • 15. 如图，△ABC中，AD⊥BC，垂足为D，AD=BD=5，CD=3，点P从点B出发沿线段BC的方向移动到点C停止，过点P作PQ⊥BC，交折线BA﹣AC于点Q，连接DQ、CQ，若△ADQ与△CDQ的面积相等，则线段BP的长度是 ．

    查看试题解析

  • 16. 如图，在第1个△ABA1中，∠B=40°，∠BAA1=∠BA1A，在A1B上取一点C，延长AA1到A2 ， 使得在第2个△A1CA2中，∠A1CA2=∠A1 A2C；在A2C上取一点D，延长A1A2到A3 ， 使得在第3个△A2DA3中，∠A2DA3=∠A2 A3D；…，按此做法进行下去，第3个三角形中以A3为顶点的内角的度数为；第n个三角形中以An为顶点的内角的度数为 ．

    查看试题解析

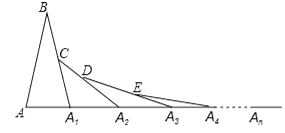
三、解答题

  • 17. 如图，已知△ABC（AC＜AB＜BC），请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：

    (1)、在边BC上确定一点P，使得PA+PC=BC；
    (2)、作出一个△DEF，使得：①△DEF是直角三角形；②△DEF的周长等于边BC的长．

    查看试题解析

  • 18. 如图，△ABC中，∠C=70°，AD、BD是△ABC的外角平分线，AD与BD交于点D，

    (1)、求∠D的度数；
    (2)、若去掉∠C=70°这个条件，试写出∠C与∠D之间的数量关系．

    查看试题解析

  • 19. 如图，已知点B，C，D，E 在同一直线上，且AB=AE，AC=AD，BD=CE．

    求证：△ABC≌△AED．

    查看试题解析

  • 20. 已知如图，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AE平分∠CAB，交CD于E，EF∥BC交AB于F，G为BC上一点，连接FG．

    (1)、求证：△AEC≌△AEF；
    (2)、若∠EFG=∠AEC，求证：FG∥AE．

    查看试题解析

  • 21. 如图，EG∥AF，请你从下面三个条件中再选两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况），并给予证明．①AB=AC，②DE=DF，③BE=CF，

    已知：EG∥AF，（   ）=（   ），（   ）=（   ）

    查看试题解析

  • 22. 如图，求作一点P，使PM=PN，并且使点P到∠AOB的两边OA，OB的距离相等．

    查看试题解析

  • 23. 如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．


    (1)、求证：△ABC≌△ADE；
    (2)、求∠FAE的度数；
    (3)、求证：CD=2BF+DE．

    查看试题解析