2018-2019学年数学浙教版八年级上册 第五章 一次函数 单元测试卷
试卷更新日期:2018-09-30 类型:单元试卷
一、选择题
-
1. 假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A、1个 B、2个 C、3个 D、4个2. 函数y= + 的自变量x的取值范围是( )A、x≥1 B、x≥1且x≠3 C、x≠3 D、1≤x≤33. 若y=(m﹣3)x+1是一次函数,则( )A、m=3 B、m=﹣3 C、m≠3 D、m≠﹣34. 一次函数y=kx+3的自变量取值增加2,函数值就相应减少2,则k的值为( )A、2 B、﹣2 C、﹣1 D、45. 如图,直线l1:y=x+1与直线l2:y=﹣x﹣ 把平面直角坐标系分成四个部分,则点( , )在( ) A、第一部分 B、第二部分 C、第三部分 D、第四部分6. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
A、第一部分 B、第二部分 C、第三部分 D、第四部分6. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( ) A、 B、 C、 D、7. 银行存款,一年定期年利率为r,取款时还要上交20%的利息税,某人存一年定期x元,到期后所得本金与利息之和为y元,则y与x之间的函数关系为( )A、y=(1+r)x B、y=(1+r)×80%x C、y=(1+r×80%)x D、y=(1+r×20%)x8. 北京奥运会吉祥物确定为象征“文化味浓、吉祥如意”的五福娃(如下图),当“五福娃”在距离北京2008奥运会整整1000天的时刻訇然问世后,不仅售出的奥运会吉祥物的数目的纪录被改写,初步推算出的超过3亿美元的效益也宣告:2008北京奥运会,已经提前打赢了第一仗!奥运爱好者小明十分喜爱福娃,于是他各买了一只福娃,已知福娃的出售价为平均每只56元,福娃的进价y与进货个数x之间的函数关系为y= (一般店家每次的进货个数最多为1399只),北京初步获得了3亿美元的效益,那么至少卖出了多少只福娃?友情提醒:1美元相当于8元人民币( )
A、 B、 C、 D、7. 银行存款,一年定期年利率为r,取款时还要上交20%的利息税,某人存一年定期x元,到期后所得本金与利息之和为y元,则y与x之间的函数关系为( )A、y=(1+r)x B、y=(1+r)×80%x C、y=(1+r×80%)x D、y=(1+r×20%)x8. 北京奥运会吉祥物确定为象征“文化味浓、吉祥如意”的五福娃(如下图),当“五福娃”在距离北京2008奥运会整整1000天的时刻訇然问世后,不仅售出的奥运会吉祥物的数目的纪录被改写,初步推算出的超过3亿美元的效益也宣告:2008北京奥运会,已经提前打赢了第一仗!奥运爱好者小明十分喜爱福娃,于是他各买了一只福娃,已知福娃的出售价为平均每只56元,福娃的进价y与进货个数x之间的函数关系为y= (一般店家每次的进货个数最多为1399只),北京初步获得了3亿美元的效益,那么至少卖出了多少只福娃?友情提醒:1美元相当于8元人民币( ) A、大于12万只小于13万只 B、大于10万只小于12万只 C、大于13万只小于14万只 D、大于9万只小于10万只9. 某校初一数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如表所示:
A、大于12万只小于13万只 B、大于10万只小于12万只 C、大于13万只小于14万只 D、大于9万只小于10万只9. 某校初一数学兴趣小组利用同一块木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度h(cm)与小车下滑时间t(s)之间的关系如表所示:支撑物高度h/cm
10
20
30
40
50
60
70
小车下滑时间t/s
4.23
3.00
2.45
2.13
1.89
1.71
1.59
根据表格提供的信息,下列说法错误的是( )
A、支撑物的高度为40cm,小车下滑时间为2.13s B、支撑物高度h越大,小车下滑时间t越小 C、若小车下滑时间为2s,则支撑物高度在40cm至50cm之间 D、若支撑物的高度为80cm,则小车下滑时间可以使小于1.59s的任意值10. 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )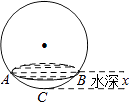 A、
A、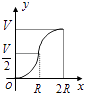 B、
B、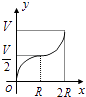 C、
C、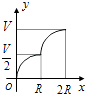 D、
D、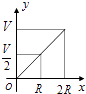
二、填空题
-
11. 正比例函数的图象是 , 当k>0时,直线y=kx过第象限,y随x的增大而 .12. 将函数y=﹣6x的图象l1向上平移5个单位得直线l2 , 则直线l2与坐标轴围成的三角形面积为 .13. 如图,直线y=2x+2 与x、y轴分别交于A、B两点,以OB为边在y轴左侧作等边△OBC,将△OBC沿y轴上下平移,使点C的对应点C′恰好落在直线AB上,则点C'的坐标为 .
 14. 若点A(m,n)在直线y=kx(k≠0)上,当﹣1≤m≤1时,﹣1≤n≤1,则这条直线的函数解析式为 .15. 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 .
14. 若点A(m,n)在直线y=kx(k≠0)上,当﹣1≤m≤1时,﹣1≤n≤1,则这条直线的函数解析式为 .15. 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为 . 16. 在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ),那么点An的纵坐标是 .
16. 在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ),那么点An的纵坐标是 .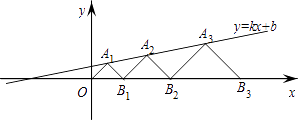
三、解答题
-
17. 已知一次函数y=kx+b的图象经过点A(0,3),B(﹣4,0).
(1)、求此函数的解析式.
(2)、若点(a,6)在此函数的图象上,求a的值为多少?(3)、求原点到直线AB的距离.18. 直线l经过(2,3)和(﹣2,﹣1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求: (1)、点A、C的坐标;
(1)、点A、C的坐标;
(2)、点B的坐标.19. 已知一次函数y=﹣ x+4的图象与x轴、y轴分别相交于点A、B,四边形AOBC(O是原点)的一组对边平行,且AC=5. (1)、求点A、B的坐标;
(1)、求点A、B的坐标;
(2)、求点C的坐标;(3)、如果一个一次函数y=kx+b(k、b为常数,且k<0)的图象经过点A、C,求这个一次函数的解析式.20. 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空: (1)、当时间为0时,甲离A地千米;(2)、当时间为时,甲、乙两人离A地距离相等;(3)、图中P点的坐标是;(4)、l1对应的函数表达式是:S1=;(5)、当t=2时,甲离A地的距离是千米;(6)、当S=28时,乙离开A地的时间是时.21. 某私营玩具厂招工广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,计件工资不少于1000元,每月另加福利工资100元,按月结算…”.该厂只生产两种玩具:小狗和小汽车,熟练工人晓凤一月份领工资1145元,她记录了如下一些数据:
(1)、当时间为0时,甲离A地千米;(2)、当时间为时,甲、乙两人离A地距离相等;(3)、图中P点的坐标是;(4)、l1对应的函数表达式是:S1=;(5)、当t=2时,甲离A地的距离是千米;(6)、当S=28时,乙离开A地的时间是时.21. 某私营玩具厂招工广告称:“本厂工人工作时间:每天工作8小时,每月工作25天;待遇:熟练工人按计件付工资,多劳多得,计件工资不少于1000元,每月另加福利工资100元,按月结算…”.该厂只生产两种玩具:小狗和小汽车,熟练工人晓凤一月份领工资1145元,她记录了如下一些数据:小狗件数(个)
小汽车数(个)
总时间(分钟)
计件工资(元)
1
1
35
2.8
2
2
70
5.6
3
2
85
6.6
(1)、根据表格中的信息,试求出做1个小汽车所需时间和计件工资各是多少?
(2)、设晓凤某月生产小狗x个,小汽车y个,月工资(计件工资+福利工资=月工资)为W元.试求W与x的函数关系式.(不需写出自变量x的取值范围)
(3)、有一天,厂方从销量方面考虑,对生产作了调整:每个工人每月生产小狗的个数不少于生产小汽车个数的2倍,假设晓凤的工作效率不变,且服从厂家安排,请运用数学知识说明厂家招工广告是否有欺诈行为.
22. 如图,在平面直角坐标系xOy中,已知正比例函数y= x与一次函数y=﹣x+7的图象交于点A. (1)、求点A的坐标;
(1)、求点A的坐标;
(2)、设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= x和y=﹣x+7的图象于点B、C,连接OC.若BC= OA,求△OBC的面积.23. “中华紫薇园”景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:可供使用人数(人/条)
价格(元/条)
长条椅
3
160
弧形椅
5
200
景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)、求景区采购了多少条长条椅,多少条弧形椅?
(2)、景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)、又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.24. 如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B. (1)、线段AB,BC,AC的长分别为AB= , BC= , AC=;(2)、折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
(1)、线段AB,BC,AC的长分别为AB= , BC= , AC=;(2)、折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由。
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A、P、C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由。