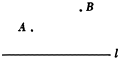2018-2019学年数学人教版（五四学制）八年级上册20.4 课题学习 最短路径问题 同步练习
试卷更新日期：2018-09-30 类型：同步测试
一、选择题
-
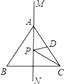
1. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是（ ）
A、30° B、15° C、20° D、35°2. 如图，∠AOB=30°，点P为∠AOB内一点，OP=10，点M、N分别在OA、OB上，求△PMN周长的最小值（ ）
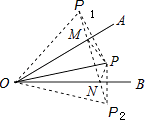A、5 B、10 C、15 D、203. 如图，在 中 ， ，面积是 ， 的垂直平分线 分别交AC，AB边于E，F点，若点 为 边的中点，点 为线段上一动点，则 周长的最小值为（ ）．
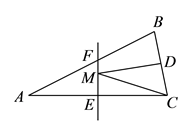A、 B、 C、 D、4. 如图，在等腰△ABC中，AB=AC=6，∠ACB=75°，AD⊥BC于D，点M、N分别是线段AB，AD上的动点，则MN+BN的最小值是（ ）
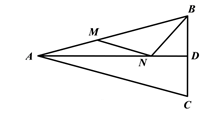A、3 B、 C、4.5 D、6二、填空题
-
5. 如图，∠AOB＝30°，点M，N分别是射线OA，OB上的动点，OP平分∠AOB，且OP＝6，△PMN的周长最小值为 ．
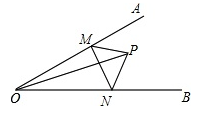
6. 如图，在等边△ABC中，AH⊥BC，垂足为H，且AH=6cm，点D是AB的中点，点P是AH上一动点，则DP与BP和的最小值是cm．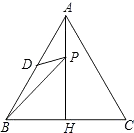
7. 如图，∠AOB=30°，点P是它内部一点，OP=2，如果点Q、点R分别是OA、OB上的两个动点，那么PQ+QR+RP的最小值是 ．
8. 如图所示，在Rt△ABC中，∠A=30°，∠B=90°，AB=12，D是斜边AC的中点，P是AB上一动点，则PC+PD的最小值为 ．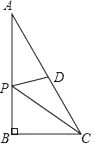
9. 如图，在四边形ABCD中，∠DAB=130°，∠D=∠B=90°，点M，N分别是CD，BC上两个动点，当△AMN的周长最小时，∠AMN+∠ANM的度数为.
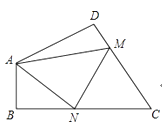10. 已知如图所示，∠MON＝40°，P为∠MON内一点，A为OM上一点，B为ON上一点，则当△PAB的周长取最小值时，∠APB的度数为 ．
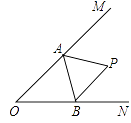11. 点A、B均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角坐标系如图所示.若P是 轴上使得∣PA—PB∣的值最大的点，Q是y轴上使得QA+QB的值最小的点，则OP·OQ=.
三、解答题
-
12. 如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：
①画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；
②在DE上画出点P，使PA+PC最小；
③在DE上画出点M，使 最大．
13. 如图，在△ABC中，D，E为AC边上的两个点，试在AB，BC上分别取一个点M，N，使四边形DMNE的周长最小.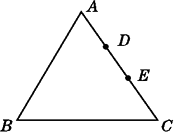
14. 如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
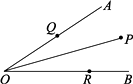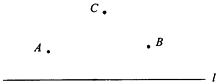
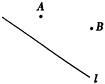
15. 最短路径问题：例：如图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短．
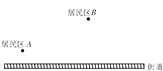
解：只有A、C、B在一直线上时，才能使AC+BC最小．作点A关于直线“街道”的对称点A′，然后连接A′B，交“街道”于点C，则点C就是所求的点．
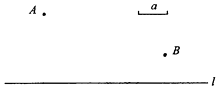
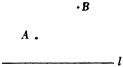
应用：已知：如图A是锐角∠MON内部任意一点，
在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小.
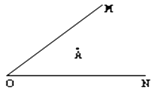(1)、借助直角三角板在下图中找出符合条件的点B和C．(2)、若∠MON=30°，OA=10，求三角形的最小周长。
